Minimale Spannbäume

图的最小生成树是总权重最小的生成树。

一个图可能有许多生成树。假设边缘被加权。最小生成树的总权重最小。例如，下图 b、c、d 中的树是图 a 中图的生成树。图c和d中的树是最小生成树。

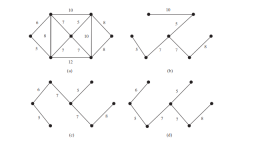
寻找最小生成树的问题有很多应用。考虑一家在许多城市设有分支机构的公司。该公司希望租用电话线将所有分支机构连接在一起。电话公司对连接不同的城市收取不同的费用。有很多方法可以将所有分支连接在一起。最便宜的方法是找到总费率最小的生成树。

最小生成树算法

如何找到最小生成树？有几种众所周知的算法可以做到这一点。本节介绍Prim算法。 Prim 的算法从包含任意顶点的生成树 T 开始。该算法通过重复添加具有与树中已有顶点相关的最低成本边的顶点来扩展树。 Prim的算法是一种贪心算法，其代码如下所示。

Input: A connected undirected weighted G = (V, E) with non-negative weights
 Output: MST (a minimum spanning tree)
 1 MST minimumSpanningTree() {
 2 Let T be a set for the vertices in the spanning tree;
 3 Initially, add the starting vertex to T;
 4
 5 while (size of T 



<p>算法首先将起始顶点添加到<strong>T</strong>中。然后，它不断地将一个顶点（例如 <strong>v</strong>）从 <strong>V – T</strong> 添加到 <strong>T</strong> 中。 <strong>v</strong> 是与 <strong>T</strong> 中的顶点相邻且边权重最小的顶点。例如，<strong>T</strong> 和 <strong>V – T</strong> 中的顶点有 5 条边连接，如下图所示，并且 (<strong>u</strong>, <strong>v</strong> ) 是权重最小的一个。</p>

<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/172557408574612.jpg?x-oss-process=image/resize,p_40" class="lazy" alt="Minimum Spanning Trees"></p>

<p>考虑下图中的图表。该算法按以下顺序将顶点添加到 <strong>T</strong>：</p>

<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/172557408660759.jpg?x-oss-process=image/resize,p_40" class="lazy" alt="Minimum Spanning Trees"></p>

<ol>
<li>将顶点 <strong>0</strong> 添加到 <strong>T</strong>。</li>
<li>将顶点 <strong>5</strong> 添加到 <strong>T</strong>，因为 <strong>Edge(5, 0, 5)</strong> 在与 T<strong>，如图a所示。从 </strong>0<strong> 到 </strong>5<strong> 的箭头线表示 </strong>0<strong> 是 </strong>5<strong> 的父级。</strong>
</li>将顶点 <li>1<strong> 添加到 </strong>T<strong>，因为 </strong>Edge(1, 0, 6)<strong> 在与 T</strong>，如图b.<strong>
</strong>将顶点 </li>6<li> 添加到 <strong>T</strong>，因为 <strong>Edge(6, 1, 7)</strong> 在与 T<strong>，如图c.</strong>
<strong>将顶点</strong>2</li>添加到<li>T<strong>，因为</strong>边（2,6,5）<strong>在与T</strong>，如图d.<strong>
</strong>将顶点<strong>4</strong>添加到</li>T<li>，因为<strong>边（4,6,7）</strong>在与T<strong>，如图e.</strong>
<strong>将顶点</strong>3<strong>添加到</strong>T</li>，因为<li>边（3,2,8）<strong>在与T</strong>，如图f.<strong>
</strong>

<strong>最小生成树不是唯一的。例如，下图中的 (c) 和 (d) 都是图 a 中的图的最小生成树。但是，如果权重不同，则该图具有唯一的最小生成树。</strong>

<strong></strong>
</li>

</ol>假设图是连通且无向的。如果图没有连通或有向，则该算法将不起作用。您可以修改算法来查找任何无向图的生成林。生成森林是一个图，其中每个连接的组件都是一棵树。<p>

</p><h2>
  
  
  Refining Prim’s MST Algorithm
</h2>

<p>To make it easy to identify the next vertex to add into the tree, we use <strong>cost[v]</strong> to store the cost of adding a vertex <strong>v</strong> to the spanning tree <strong>T</strong>. Initially <strong>cost[s]</strong> is <strong>0</strong> for a starting vertex and assign infinity to <strong>cost[v]</strong> for all other vertices. The algorithm repeatedly finds a vertex <strong>u</strong> in <strong>V – T</strong> with the smallest <strong>cost[u]</strong> and moves <strong>u</strong> to <strong>T</strong>. The refined version of the alogrithm is given in code below.<br>
</p>

<pre class="brush:php;toolbar:false">Input: A connected undirected weighted G = (V, E) with non-negative weights
Output: a minimum spanning tree with the starting vertex s as the root
 1 MST getMinimumSpanngingTree(s) {
 2 Let T be a set that contains the vertices in the spanning tree;
 3 Initially T is empty;
 4 Set cost[s] = 0; and cost[v] = infinity for all other vertices in V;
 5
 6 while (size of T  w(u, v)) { // Adjust cost[v]
11 cost[v] = w(u, v); parent[v] = u;
12 }
13 }
14 }

Implementation of the MST Algorithm

The getMinimumSpanningTree(int v) method is defined in the WeightedGraph class. It returns an instance of the MST class, as shown in Figure below.

The MST class is defined as an inner class in the WeightedGraph class, which extends the Tree class, as shown in Figure below.

The Tree class was shown in Figure below. The MST class was implemented in lines 141–153 in WeightedGraph.java.

The refined version of the Prim’s algoruthm greatly simplifies the implementation. The getMinimumSpanningTree method was implemented using the refined version of the Prim’s algorithm in lines 99–138 in Listing 29.2. The getMinimumSpanningTree(int startingVertex) method sets cost[startingVertex] to 0 (line 105) and cost[v] to infinity for all other vertices (lines 102–104). The parent of startingVertex is set to -1 (line 108). T is a list that stores the vertices added into the spanning tree (line 111). We use a list for T rather than a set in order to record the order of the vertices added to T.

Initially, T is empty. To expand T, the method performs the following operations:

1. Find the vertex u with the smallest cost[u] (lines 118–123 and add it into T (line 125).
2. After adding u in T, update cost[v] and parent[v] for each v adjacent to u in V-T if cost[v] > w(u, v) (lines 129–134).

After a new vertex is added to T, totalWeight is updated (line 126). Once all vertices are added to T, an instance of MST is created (line 137). Note that the method will not work if the graph is not connected. However, you can modify it to obtain a partial MST.

The MST class extends the Tree class (line 141). To create an instance of MST, pass root, parent, T, and totalWeight (lines 144-145). The data fields root, parent, and searchOrder are defined in the Tree class, which is an inner class defined in AbstractGraph.

Note that testing whether a vertex i is in T by invoking T.contains(i) takes O(n) time, since T is a list. Therefore, the overall time complexity for this implemention is O(n3).

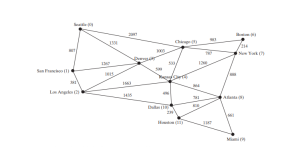
The code below gives a test program that displays minimum spanning trees for the graph in Figure below and the graph in Figure below a, respectively.

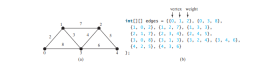
package demo;

public class TestMinimumSpanningTree {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph<string> graph1 = new WeightedGraph(vertices, edges);
        WeightedGraph<string>.MST tree1 = graph1.getMinimumSpanningTree();
        System.out.println("Total weight is " + tree1.getTotalWeight());
        tree1.printTree();

        edges = new int[][]{
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };

        WeightedGraph<integer> graph2 = new WeightedGraph(edges, 5);
        WeightedGraph<integer>.MST tree2 = graph2.getMinimumSpanningTree(1);
        System.out.println("\nTotal weight is " + tree2.getTotalWeight());
        tree2.printTree();
    }

}

</integer></integer></string></string>

Total weight is 6513.0
Root is: Seattle
Edges: (Seattle, San Francisco) (San Francisco, Los Angeles)
(Los Angeles, Denver) (Denver, Kansas City) (Kansas City, Chicago)
(New York, Boston) (Chicago, New York) (Dallas, Atlanta)
(Atlanta, Miami) (Kansas City, Dallas) (Dallas, Houston)

Total weight is 14.0
Root is: 1
Edges: (1, 0) (3, 2) (1, 3) (2, 4)

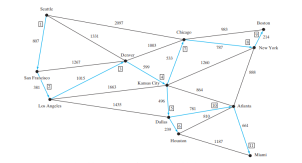
Das Programm erstellt in Zeile 27 ein gewichtetes Diagramm für die obige Abbildung. Anschließend ruft es getMinimumSpanningTree() (Zeile 28) auf, um einen MST zurückzugeben, der einen minimalen Spannbaum für darstellt Graph. Durch Aufrufen von printTree() (Zeile 30) für das MST-Objekt werden die Kanten im Baum angezeigt. Beachten Sie, dass MST eine Unterklasse von Tree ist. Die Methode printTree() ist in der Klasse Tree definiert.

Die grafische Darstellung des minimalen Spannbaums ist in der Abbildung unten dargestellt. Die Eckpunkte werden in dieser Reihenfolge zum Baum hinzugefügt: Seattle, San Francisco, Los Angeles, Denver, Kansas City, Dallas, Houston, Chicago, New York, Boston, Atlanta und Miami.

Das obige ist der detaillierte Inhalt vonMinimale Spannbäume. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!