Die WeightedGraph-Klasse

Die Klasse WeightedGraph erweitert AbstractGraph.
Im vorherigen Kapitel wurden die Schnittstelle Graph, die Klasse AbstractGraph und die Klasse UnweightedGraph für die Modellierung von Diagrammen entworfen. Nach diesem Muster entwerfen wir WeightedGraph als Unterklasse von AbstractGraph, wie in der Abbildung unten gezeigt.

WeightedGraph erweitert einfach AbstractGraph um fünf Konstruktoren zum Erstellen konkreter WeightedGraph-Instanzen. WeightedGraph erbt alle Methoden von AbstractGraph, überschreibt die Methoden clear und addVertex und implementiert eine neue addEdge-Methode für Hinzufügen einer gewichteten Kante und Einführung neuer Methoden zum Erhalten minimaler Spannbäume und zum Finden aller kürzesten Pfade aus einer Quelle. Minimale Spannbäume und kürzeste Pfade werden in den Abschnitten Minimale Spannbäume und kürzeste Pfade eingeführt.

Der folgende Code implementiert WeightedGraph. Kantenadjazenzlisten (Zeilen 38–63) werden intern verwendet, um benachbarte Kanten für einen Scheitelpunkt zu speichern. Wenn ein WeightedGraph erstellt wird, werden seine Kantenadjazenzlisten erstellt (Zeilen 47 und 57). Die Methoden getMinimumSpanningTree() (Zeilen 99–138) und getShortestPath() (Zeilen 156–197) werden in den kommenden Abschnitten vorgestellt.

package demo;
import java.util.*;

public class WeightedGraph<V> extends AbstractGraph<V> {
    /** Construct an empty */
    public WeightedGraph() {}

    /** Construct a WeightedGraph from vertices and edged in arrays */
    public WeightedGraph(V[] vertices, int[][] edges) {
        createWeightedGraph(java.util.Arrays.asList(vertices), edges);
    }

     /** Construct a WeightedGraph from vertices and edges in list */
    public WeightedGraph(int[][] edges, int numberOfVertices) {
        List<V> vertices = new ArrayList<>();
        for (int i = 0; i < numberOfVertices; i++)
            vertices.add((V)(new Integer(i)));

        createWeightedGraph(vertices, edges);
    }

    /** Construct a WeightedGraph for vertices 0, 1, 2 and edge list */
    public WeightedGraph(List<V> vertices, List<WeightedEdge> edges) {
        createWeightedGraph(vertices, edges);
    }

    /** Construct a WeightedGraph from vertices 0, 1, and edge array */
    public WeightedGraph(List<WeightedEdge> edges, int numberOfVertices) {
        List<V> vertices = new ArrayList<>();
        for (int i = 0; i < numberOfVertices; i++)
            vertices.add((V)(new Integer(i)));

        createWeightedGraph(vertices, edges);
    }

    /** Create adjacency lists from edge arrays */
    private void createWeightedGraph(List<V> vertices, int[][] edges) {
        this.vertices = vertices;

        for (int i = 0; i < vertices.size(); i++) {
            neighbors.add(new ArrayList<Edge>()); // Create a list for vertices
        }

        for (int i = 0; i < edges.length; i++) {
            neighbors.get(edges[i][0]).add(new WeightedEdge(edges[i][0], edges[i][1], edges[i][2]));
        }
    }

    /** Create adjacency lists from edge lists */
    private void createWeightedGraph(List<V> vertices, List<WeightedEdge> edges) {
        this.vertices = vertices;

        for (int i = 0; i < vertices.size(); i++) {
            neighbors.add(new ArrayList<Edge>()); // Create a list for vertices
        }

        for (WeightedEdge edge: edges) {
            neighbors.get(edge.u).add(edge); // Add an edge into the list
        }
    }

    /** Return the weight on the edge (u, v) */
    public double getWeight(int u, int v) throws Exception {
        for (Edge edge : neighbors.get(u)) {
            if (edge.v == v) {
                return ((WeightedEdge)edge).weight;
            }
        }

        throw new Exception("Edge does not exit");
    }

    /** Display edges with weights */
    public void printWeightedEdges() {
        for (int i = 0; i < getSize(); i++) {
            System.out.print(getVertex(i) + " (" + i + "): ");
            for (Edge edge : neighbors.get(i)) {
                System.out.print("(" + edge.u + ", " + edge.v + ", " + ((WeightedEdge)edge).weight + ") ");
            }

            System.out.println();
        }
    }

    /** Add edges to the weighted graph */
    public boolean addEdge(int u, int v, double weight) {
        return addEdge(new WeightedEdge(u, v, weight));
    }

    /** Get a minimum spanning tree rooted at vertex 0 */
    public MST getMinimumSpanningTree() {
        return getMinimumSpanningTree(0);
    }

    /** Get a minimum spanning tree rooted at a specified vertex */
    public MST getMinimumSpanningTree(int startingVertex) {
        // cost[v] stores the cost by adding v to the tree
        double[] cost = new double[getSize()];
        for (int i = 0; i < cost.length; i++) {
            cost[i] = Double.POSITIVE_INFINITY; // Initial cost
        }
        cost[startingVertex] = 0; // Cost of source is 0

        int[] parent = new int[getSize()]; // Parent of a vertex
        parent[startingVertex] = -1; // startingVertex is the root
        double totalWeight = 0; // Total weight of the tree thus far

        List<Integer> T = new ArrayList<>();

        // Expand T
        while (T.size() < getSize()) {
            // Find smallest cost v in V - T
            int u = -1; // Vertex to be determined
            double currentMinCost = Double.POSITIVE_INFINITY;
            for (int i = 0; i < getSize(); i++) {
                if (!T.contains(i) && cost[i] < currentMinCost) {
                    currentMinCost = cost[i];
                    u = i;
                }
            }

            T.add(u); // Add a new vertex to T
            totalWeight += cost[u]; // Add cost[u] to the tree

            // Adjust cost[v] for v that is adjacent to u and v in V - T
            for (Edge e : neighbors.get(u)) {
                if (!T.contains(e.v) && cost[e.v] > ((WeightedEdge)e).weight) {
                    cost[e.v] = ((WeightedEdge)e).weight;
                    parent[e.v] = u;
                }
            }
        } // End of while

        return new MST(startingVertex, parent, T, totalWeight);
    }

    /** MST is an inner class in WeightedGraph */
    public class MST extends Tree {
        private double totalWeight; // Total weight of all edges in the tree

        public MST(int root, int[] parent, List<Integer> searchOrder, double totalWeight) {
            super(root, parent, searchOrder);
            this.totalWeight = totalWeight;
        }

        public double getTotalWeight() {
            return totalWeight;
        }
    }

    /** Find single source shortest paths */
    public ShortestPathTree getShortestPath(int sourceVertex) {
        // cost[v] stores the cost of the path from v to the source
        double[] cost = new double[getSize()];
        for (int i = 0; i < cost.length; i++) {
            cost[i] = Double.POSITIVE_INFINITY; // Initial cost set to infinity
        }
        cost[sourceVertex] = 0; // Cost of source is 0

        // parent[v] stores the previous vertex of v in the path
        int[] parent = new int[getSize()];
        parent[sourceVertex] = -1; // The parent of source is set to -1

        // T stores the vertices whose path found so far
        List<Integer> T = new ArrayList<>();

        // Expand T
        while (T.size() < getSize()) {
            // Find smallest cost v in V - T
            int u = -1; // Vertex to be determined
            double currentMinCost = Double.POSITIVE_INFINITY;
            for (int i = 0; i < getSize(); i++) {
                if (!T.contains(i) && cost[i] < currentMinCost) {
                    currentMinCost = cost[i];
                    u = i;
                }
            }

            T.add(u); // Add a new vertex to T

            // Adjust cost[v] for v that is adjacent to u and v in V - T
            for (Edge e : neighbors.get(u)) {
                if (!T.contains(e.v) && cost[e.v] > cost[u] + ((WeightedEdge)e).weight) {
                    cost[e.v] = cost[u] + ((WeightedEdge)e).weight;
                    parent[e.v] = u;
                }
            }
        } // End of while

        // Create a ShortestPathTree
        return new ShortestPathTree(sourceVertex, parent, T, cost);
    }

    /** ShortestPathTree is an inner class in WeightedGraph */
    public class ShortestPathTree extends Tree {
        private double[] cost; // cost[v] is the cost from v to source

        /** Construct a path */
        public ShortestPathTree(int source, int[] parent, List<Integer> searchOrder, double[] cost) {
            super(source, parent, searchOrder);
            this.cost = cost;
        }

        /** Return the cost for a path from the root to vertex v */
        public double getCost(int v) {
            return cost[v];
        }

        /** Print paths from all vertices to the source */
        public void printAllPaths() {
            System.out.println("All shortest paths from " + vertices.get(getRoot()) + " are:");
            for (int i = 0; i < cost.length; i++) {
                printPath(i); // Print a path from i to the source
                System.out.println("(cost: " + cost[i] + ")"); // Path cost
            }
        }
    }
}

Die Klasse WeightedGraph erweitert die Klasse AbstractGraph (Zeile 3). Die Eigenschaften vertices und neighbors in AbstractGraph werden in WeightedGraph.neighbors vererbt, einer Liste. Jedes Element der Liste ist eine andere Liste, die Kanten enthält. Bei einem ungewichteten Diagramm ist jede Kante eine Instanz von AbstractGraph.Edge. Bei einem gewichteten Diagramm ist jede Kante eine Instanz von WeightedEdge. WeightedEdge ist ein Untertyp von Edge. Sie können also eine gewichtete Kante in neighbors.get(i) für einen gewichteten Graphen hinzufügen (Zeile 47).

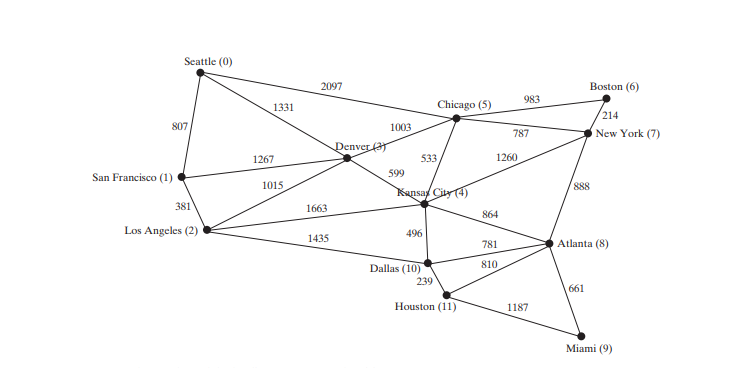
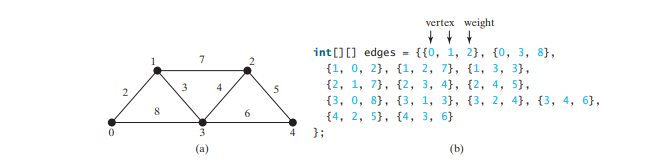
Der folgende Code gibt ein Testprogramm an, das ein Diagramm für das in Abbildung unten und ein weiteres Diagramm für das in Abbildung unten a erstellt.

package demo;

public class TestWeightedGraph {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph<String> graph1 = new WeightedGraph<>(vertices, edges);
        System.out.println("The number of vertices in graph1: " + graph1.getSize());
        System.out.println("The vertex with index 1 is " + graph1.getVertex(1));
        System.out.println("The index for Miami is " + graph1.getIndex("Miami"));
        System.out.println("The edges for graph1:");
        graph1.printWeightedEdges();

        edges = new int[][] {
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };
        WeightedGraph<Integer> graph2 = new WeightedGraph<>(edges, 5);
        System.out.println("\nThe edges for graph2:");
        graph2.printWeightedEdges();
    }
}

Die Anzahl der Eckpunkte in Diagramm1: 12
Der Scheitelpunkt mit Index 1 ist San Francisco
Der Index für Miami ist 9
Die Kanten für graph1:
Scheitelpunkt 0: (0, 1, 807) (0, 3, 1331) (0, 5, 2097)
Scheitelpunkt 1: (1, 2, 381) (1, 0, 807) (1, 3, 1267)
Scheitelpunkt 2: (2, 1, 381) (2, 3, 1015) (2, 4, 1663) (2, 10, 1435)
Scheitelpunkt 3: (3, 4, 599) (3, 5, 1003) (3, 1, 1267)
(3, 0, 1331) (3, 2, 1015)
Scheitelpunkt 4: (4, 10, 496) (4, 8, 864) (4, 5, 533) (4, 2, 1663)
(4, 7, 1260) (4, 3, 599)
Scheitelpunkt 5: (5, 4, 533) (5, 7, 787) (5, 3, 1003)
(5, 0, 2097) (5, 6, 983)
Scheitelpunkt 6: (6, 7, 214) (6, 5, 983)
Scheitelpunkt 7: (7, 6, 214) (7, 8, 888) (7, 5, 787) (7, 4, 1260)
Scheitelpunkt 8: (8, 9, 661) (8, 10, 781) (8, 4, 864)
(8, 7, 888) (8, 11, 810)
Scheitelpunkt 9: (9, 8, 661) (9, 11, 1187)
Scheitelpunkt 10: (10, 11, 239) (10, 4, 496) (10, 8, 781) (10, 2, 1435)
Scheitelpunkt 11: (11, 10, 239) (11, 9, 1187) (11, 8, 810)

Die Kanten für Graph2:
Scheitelpunkt 0: (0, 1, 2) (0, 3, 8)
Scheitelpunkt 1: (1, 0, 2) (1, 2, 7) (1, 3, 3)
Scheitelpunkt 2: (2, 3, 4) (2, 1, 7) (2, 4, 5)
Scheitelpunkt 3: (3, 1, 3) (3, 4, 6) (3, 2, 4) (3, 0, 8)
Scheitelpunkt 4: (4, 2, 5) (4, 3, 6)

Das Programm erstellt graph1 für den Graphen in Abbildung oben in den Zeilen 3–27. Die Eckpunkte für graph1 werden in den Zeilen 3–5 definiert. Die Kanten für graph1 werden in den Zeilen 7–24 definiert. Die Kanten werden durch ein zweidimensionales Array dargestellt. Für jede Zeile i im Array geben edges[i][0] und edges[i][1] an, dass es eine Kante vom Scheitelpunkt edges[i] gibt. [0] zum Scheitelpunkt edges[i][1] und das Gewicht für die Kante ist edges[i][2]. Beispielsweise repräsentiert {0, 1, 807} (Zeile 8) die Kante vom Scheitelpunkt 0 (Kanten[ 0][0]) zu Scheitelpunkt 1 (Kanten[0][1]) mit Gewicht 807 (Kanten[0] [2]). {0, 5, 2097} (Zeile 8) stellt die Kante vom Scheitelpunkt 0 dar (Kanten[2][ 0]) zu Scheitelpunkt 5 (Kanten[2][1]) mit Gewicht 2097 (Kanten[2][2] ). Zeile 35 ruft die Methode printWeightedEdges() für graph1 auf, um alle Kanten in graph1 anzuzeigen.

Das Programm erstellt die Kanten für graph2 für den Graphen in Abbildung oben a in den Zeilen 37–44. Zeile 46 ruft die Methode printWeightedEdges() für graph2 auf, um alle Kanten in graph2 anzuzeigen.

Das obige ist der detaillierte Inhalt vonDie WeightedGraph-Klasse. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!