Fibonacci-Reihe in C#

Die Fibonacci-Reihe in C# in der Fibonacci-Reihe ist eine der bekanntesten Sequenzreihen. Die Reihenfolge ist 0, 1, 1, 2, 3, 5, 8…. Die Fibonacci-Reihe beginnt bei Null und Eins und die nächste Zahl ist die Summe zweier vorhergehender Zahlen. Es heißt, dass die Fibonacci-Reihe im 13. Jahrhundert von Leonardo Pisano Bigollo geschaffen wurde. Für einige Szenarien ist die Fibonacci-Reihe nützlich. Grundsätzlich wurde es ursprünglich zur Lösung des Kaninchenproblems verwendet, d. h. der Anzahl der aus einem Paar geborenen Kaninchen. Es gibt auch andere Probleme, bei denen die Fibonacci-Folge nützlich ist. Logik der Fibonacci-Reihe

Wie in der Fibonacci-Reihe ist die Zahl die Summe ihrer beiden vorhergehenden Zahlen. Wenn wir also eine Fibonacci-Reihe haben, sagen wir 0, 1, 1, 2, 3, 5, 8, 13, 21 ... Demnach wäre die nächste Zahl die Summe der beiden vorhergehenden Zahlen wie 13 und 21. Die nächste Zahl ist also 13 +21=34.

Hier ist die Logik zum Generieren von Fibonacci-Reihen

F(n)= F(n-1) +F(n-2)

Wobei F(n) die Termnummer und F(n-1) +F(n-2) eine Summe vorhergehender Werte ist.

Wenn wir also die Serien 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 haben …

Gemäß der Logik F(n)= F(n-1) +F(n-2)

F(n)= 55+89

F(n)= 144

Der nächste Begriff wäre 144.

Verschiedene Methoden zur Erstellung von Fibonacci-Reihen

Fibonacci-Reihen können auf verschiedene Arten generiert werden.

1. Iterativer Ansatz

Dieser Weg ist der einfachste Weg, Serien zu generieren.

Code:

2. Rekursive Methode

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceFibonacciDemo
{
classProgram
{
staticint Fibonacci(int n)
{
intfirstnumber = 0, secondnumber = 1, result = 0;
if (n == 0) return 0; //It will return the first number of the series
if (n == 1) return 1; // it will return  the second number of the series
for (int i = 2; i<= n; i++)  // main processing starts from here
{
result = firstnumber + secondnumber;
firstnumber = secondnumber;
secondnumber = result;
}
return result;
}
staticvoid Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
for(int i = 0; i< length; i++)
{
Console.Write("{0} ", Fibonacci(i));
}
Console.ReadKey();
}
}
}

Dies ist eine weitere Methode zur Lösung dieses Problems.

Methode 1

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceFibonacciDemo
{
classProgram
{
staticint Fibonacci(int n)
{
intfirstnumber = 0, secondnumber = 1, result = 0;
if (n == 0) return 0; //it will return the first number of the series
if (n == 1) return 1; // it will return the second number of the series
return Fibonacci(n-1) + Fibonacci(n-2);
}
staticvoid Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
for(int i = 0; i< length; i++)
{
Console.Write("{0} ", Fibonacci(i));
}
Console.ReadKey();
}
}
}

Methode 2

using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FibonacciSeries
{
class Program
{
public static void Fibonacci
(
int firstnumber,
int secondnumber,
int count,
int length,
)
{
if (count <= length)
{
Console.Write("{0} ", firstnumber);
Fibonacci(secondnumber, firstnumber + secondnumber, count + 1, length);
}
}
public static void Main(string[] args)
{
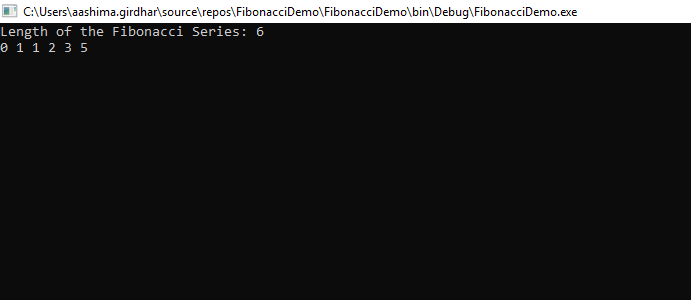
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
Fibonacci(0, 1, 1, length);
Console.ReadKey();
}
}
}

Ausgabe:

3. Fibonacci mithilfe von Array

Code:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
public class Program
{
public static int[] Fibonacci(int number)
{
int[] a = new int[number];
a[0] = 0;
a[1] = 1;
for (int i = 2; i < number; i++)
{
a[i] = a[i - 2] + a[i - 1];
}
return a;
}
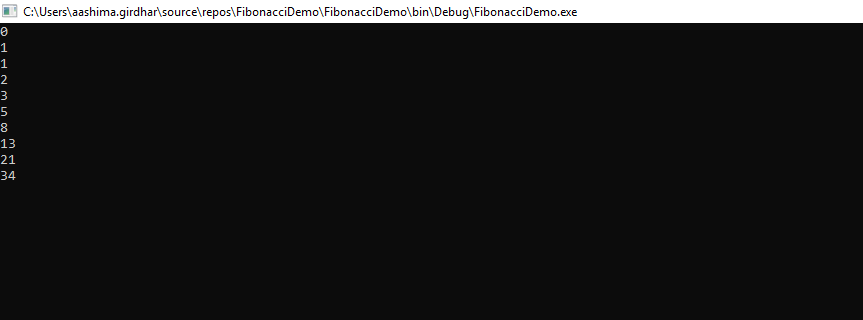
public static void Main(string[] args)
{
var b = Fibonacci(10);
foreach (var elements in b)
{
Console.WriteLine(elements);
}
}
}

Ausgabe:

Wie finde ich den N-ten Term der Fibonacci-Reihe?

Folgend sind die Methoden

Methode 1

Code:

Der obige Code dient dazu, den n-ten Term in der Fibonacci-Reihe zu finden. Wenn wir beispielsweise den 12

using System;
namespace FibonacciSeries
{
class Program {
public static int NthTerm(int n)
{
if ((n == 0) || (n == 1))
{
return n;
}
else
{
return (NthTerm(n - 1) + NthTerm(n - 2));
}
}
public static void Main(string[] args)
{
Console.Write("Enter the nth term of the Fibonacci Series: ");
int number = Convert.ToInt32(Console.ReadLine());
number = number - 1;
Console.Write(NthTerm(number));
Console.ReadKey();
}
}
}

ten

Term in der Reihe finden möchten, wäre das Ergebnis 89. Methode 2

(O(Log t) Zeit).

Es gibt eine weitere Rekursionsformel, die verwendet werden kann, um die t-te Fibonacci-Zahl zu ermitteln. Wenn t gerade ist, dann = t/2:

F(t) = [2*F(k-1) + F(k)]*F(k)

Wenn t ungerade ist, dann ist k = (t + 1)/2

F(t) = F(k)*F(k) + F(k-1)*F(k-1)

Fibonacci-Matrix

Nachdem wir die Determinante erhalten haben, erhalten wir (-1)t = Ft+1Ft-1 – Ft2

FmFt + Fm-1Ft-1 = Fm+t-1

Indem man t = t+1 setzt,

FmFt+1 + Fm-1Ft = Fm+t

Setzen Sie m = t

F2t-1 = Ft2 + Ft-12

F2t = (Ft-1 + Ft+1)Ft = (2Ft-1 + Ft)Ft

Um die Formel zu erhalten, gehen wir wie folgt vor

Wenn t gerade ist, setzen Sie k = t/2

Wenn t ungerade ist, setzen Sie k = (t+1)/2

Durch das Sortieren dieser Zahlen können wir verhindern, dass der Speicherplatz von STACK ständig belegt wird. Es gibt die Zeitkomplexität von O(n) an. Der rekursive Algorithmus ist weniger effizient.

Code:

Wenn nun der obige Algorithmus für n=4 ausgeführt wird

int f(n) :
if( n==0 || n==1 )
return n;
else
return f(n-1) + f(n-2)

fn(4)

f(3)             f(2)

f(2)   f(1)     f(1)   f(0)

f(1)  f(0)

Es ist also ein Baum. Zur Berechnung von f(4) müssen wir f(3) und f(2) usw. berechnen. Für einen kleinen Wert von 4 wird f(2) zweimal und f(1) dreimal berechnet. Diese Anzahl der Ergänzungen wird bei großen Zahlen zunehmen.

Es gibt eine Vermutung, dass die Anzahl der zur Berechnung von f (n) erforderlichen Additionen f (n+1) -1 beträgt.

Fazit

Hier wird immer die Iterationsmethode bevorzugt, da sie einen schnelleren Ansatz zur Lösung dieser Art von Problemen bietet. Hier speichern wir die erste und die zweite Zahl der Fibonacci-Reihe in der vorherigen Zahl und der vorherigen Zahl (das sind zwei Variablen) und verwenden außerdem die aktuelle Zahl, um die Fibonacci-Zahl zu speichern.

Das obige ist der detaillierte Inhalt vonFibonacci-Reihe in C#. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!