Matrixmultiplikation in Java

Matrizen in Java werden in Arrays gespeichert. Es gibt eindimensionale und zweidimensionale Arrays, die Werte in Form von Matrizen in den als Arrays bezeichneten Dimensionen speichern. In einem eindimensionalen Array werden nur eindimensionale Zahlen gespeichert, während in zweidimensionalen Arrays Zahlen in Form von Zeilen und Spalten gespeichert werden. Mit Matrizen können in der Programmiersprache Java Zahlen addiert, subtrahiert und multipliziert werden. Die Matrixmultiplikation ist eine der kompliziertesten Aufgaben in der Java-Programmiermethodik. In diesem Artikel müssen wir eine Matrixmultiplikation in Java durchführen und zeigen, wie wir zwei Matrizen multiplizieren und eine vernünftige Ausgabe liefern können.

Starten Sie Ihren kostenlosen Softwareentwicklungskurs

Webentwicklung, Programmiersprachen, Softwaretests und andere

Allgemeine Methodik

Die Matrixmultiplikation in der Programmiersprache Java erfolgt auf sehr einfache Weise. Zuerst geben wir die Zahlen in das erste zweidimensionale Array ein und dann geben wir die Nummern der Elemente in das zweite zweidimensionale Array ein. Die Zahlen werden zeilenweise addiert, das heißt, die erste Zeile wird erstellt, dann werden die Zahlen in der zweiten Zeile erstellt und so weiter. Dann wird die zweite Matrix auf ähnliche Weise erstellt und dann beginnen wir mit der Multiplikation der Zahlen in den Matrizen.

Beispiele für Matrixmultiplikation in Java

Nachfolgend finden Sie Beispiele für die Matrixmultiplikation

Beispiel #1

Im Codierungsbeispiel sehen wir, wie zwei Matrizen zeilenweise eingegeben werden und anschließend die Matrixmultiplikation durchgeführt wird. Der Code für die Multiplikation zweier Matrizen ist unten dargestellt. Es sind drei Arrays deklariert. Das Produkt der ersten und zweiten Matrize wird in der dritten Matrix angezeigt. Dann wird die Matrix als Ausgabe angezeigt, die ein Produkt zweier Matrizen im Array ist.

Code:

import java.util.Scanner;
public class MatixMultiplication
{
public static void main(String args[])
{
int n;
Scanner input = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of the matrices. They must be equal.");
n = input.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int[][] c = new int[n][n];
System.out.println("Enter the numbers of the first matrix. Numbers will be added row wise \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = input.nextInt();
}
}
System.out.println("Enter the numbers of the 2nd matrix. Numbers will be added row wise.  \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
b[i][j] = input.nextInt();
}
}
System.out.println("Generating the multiplication of matrices.....");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}
}
}
System.out.println("The product of the matrices is shown as below");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
System.out.print(c[i][j] + " ");
}
System.out.println();
}
input.close();
}
}

Die Ausgabe für eine 2*2-Matrix wird angezeigt. Die erste Matrix besteht aus Elementen wie { 1,2

3,4}

und auch die zweite Matrix enthält die gleichen Elemente. In der Beispielausgabe bemerken wir die Multiplikation der Matrizen und der Beispielausgabe. Die Elemente der Matrix sind auf sehr schöne Weise hergestellt. Die erzeugte Ausgabe

{1,2                          { 1,2                                     { 7, 10

3,4}        *                3,4}              =                       15, 22}

Ausgabe:

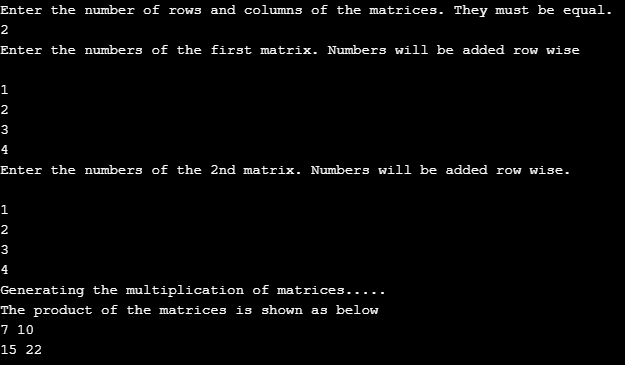
Beispiel #2

In Codierungsbeispiel 2 haben wir das gleiche Programm, aber jetzt verwenden wir dreidimensionale Arrays zur Multiplikation. Wir verwenden jetzt die 3 * 3-Matrixmultiplikation und zeigen die Ausgabe in einem anderen dreidimensionalen Array.

Code:

import java.util.Scanner;
public class Matix
{
public static void main(String args[])
{
int n;
Scanner input = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of the matrices. They must be equal.");
n = input.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int[][] c = new int[n][n];
System.out.println("Enter the numbers of the first matrix. Numbers will be added row wise \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = input.nextInt();
}
}
System.out.println("Enter the numbers of the 2nd matrix. Numbers will be added row wise.  \n");
for (int z = 0; z < n; z++)
{
for (int k = 0; k < n; k++)
{
b[z][k] = input.nextInt();
}
}
System.out.println("Generating the multiplication of matrices.....");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}
}
}
System.out.println("The product of the matrices is shown as below");
for (int k = 0; k < n; k++)
{
for (int l = 0; l < n; l++)
{
System.out.print(c[k][l] + " ");
}
System.out.println();
}
input.close();
}
}

Aus dem zweiten Beispielcode drucken wir zwei 3 * 3-Matrizen. Die erste Matrix ist {1,1,1

1,1,1

1,1,1}

und die zweite Matrix ist auch dieselbe. Die Matrixmultiplikation wird auf folgende Weise generiert

{1,1,1                          {1,1,1                                               { 3,3,3

1,1,1                *         1,1,1                                  =              3,3,3

1,1,1}                          1,1,1}                                               3,3,3

Ausgabe:

Fazit

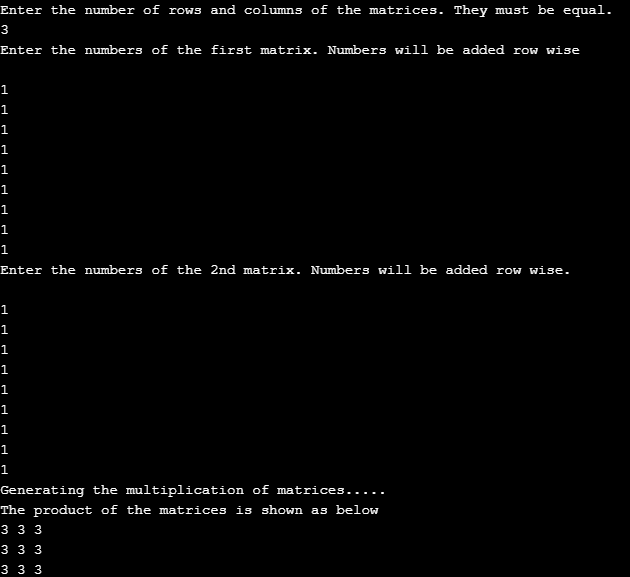
In diesem Artikel sehen wir die Multiplikation einer 2 * 2-Matrix und einer 3 * 3-Matrix und die Ausgabe wird auf sehr schöne Weise dargestellt. Die Ergebnisse sind übersichtlich dargestellt. Mithilfe der Matrixmultiplikation können wir auch eine 4*4-Multiplikation einer Matrix erstellen. Im ersten Schritt des Programms wird die Basis abgefragt. Wir können auch 5 * 5, 6 * 6 Matrizen erstellen. Die Komplexität des Programms ist umso wichtiger.

Die einfache Multiplikation von Matrizen ist jedoch sehr nützlich, um die Spiegelung eines Punktes mit der X-Achse, der Y-Achse oder der Z-Achse als Spiegelungsachse zu berechnen. Diese einfachen Konzepte werden in der Koordinatengeometrie und in der mathematischen Modellierung von Geometrieanwendungen verwendet.

Das obige ist der detaillierte Inhalt vonMatrixmultiplikation in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!