Heim >Java >javaLernprogramm >Rekursion in Java
Rekursion in Java
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2024-08-30 15:33:33430Durchsuche
Rekursion ist in Java definiert als „eine Methode ruft sich selbst (dieselbe Methode) kontinuierlich direkt oder indirekt auf.“ Eine Rekursionsfunktion wird in Situationen verwendet, in denen dieselben Operationen immer wieder ausgeführt werden müssen, bis das Ergebnis erreicht ist. Es führt mehrere Iterationen durch und die Problemstellung wird mit jeder Iteration immer einfacher. Rekursion in Java ist eine Methode zur Lösung des Problems, die auf der Lösung des kleineren Blocks desselben Problems basiert. Die meisten Iterationen mit unendlichen Möglichkeiten können durch Rekursion gelöst werden. Wir können sagen, dass Rekursion eine Alternative zu Schleifenanweisungen ist. Wenn wir die rekursive Funktion nicht richtig verwendet haben, wird sie unendlich oft ausgeführt.
Syntax:
WERBUNG Beliebter Kurs in dieser Kategorie JAVA MASTERY - Spezialisierung | 78 Kursreihe | 15 Probetestsreturntype methodName()
{
//logic for application
methodName();//recursive call
}
Wie können wir unendliche Rekursionsbedingungen in Java stoppen?
Um die unendlichen Bedingungen zu stoppen, müssen wir Folgendes haben:
- Grundbedingung: Geben Sie darin an, ob die Bedingung die Rekursionsfunktion stoppen würde.
- Rekursionsaufruf: Richtiger Rekursionsaufruf.
Wir können eine Rekursionsfunktion auf zwei Arten aufrufen:
1. Direkter Rekursionsaufruf
Wenn wir dieselbe Methode aus dem inneren Methodenkörper aufrufen.
Syntax:
returntype methodName()
{
//logic for application
methodName();//recursive call
}
Beispiel:
Fakultät einer Zahl ist ein Beispiel für eine direkte Rekursion. Das Grundprinzip der Rekursion besteht darin, ein komplexes Problem durch die Aufteilung in kleinere zu lösen. Im Fall der Fakultät einer Zahl berechnen wir beispielsweise die Fakultät von „i“, wenn wir deren Fakultät „i-1“ kennen.
Code:
public class Factorial {
static int fact(int i){
if (i == 1)
return 1;
else
return(i * fact(i-1));
}
public static void main(String[] args) {
System.out.println("The factorial of given number 6 is: "+fact(6));
}
}
Ausgabe:

2. Indirekter/gegenseitiger Rekursionsaufruf
Wenn wir eine Methode von einer anderen Methode aufrufen und eine andere Methode von der ersten Methode aufgerufen wird, ist das umgekehrt.
Syntax:
<firstIndirectRecursive()
{
// Logic
secondIndirectRecursive();
}
secondIndirectRecursive()
{
//Logic
firstIndirectRecursive();
}
Beispiel:
Um die indirekte Rekursion zu zeigen, verwenden wir das folgende Programm, mit dem anhand der gegebenen Eingabe ermittelt werden kann, ob eine bestimmte Zahl gerade oder ungerade ist.
Code:
import java.util.Scanner;
public class IndirectRecursion {
public static boolean oddNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return false;
} else {
return evenNum(i-1);
}
}
public static boolean evenNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return true;
} else {
return oddNum(i-1);
}
}
public static void main(String[] args) {
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
}
}
Ausgabe:
Beispiele für Rekursion in Java
Hier sind einige weitere Beispiele zur Lösung der Probleme mit der Rekursionsmethode.
Beispiel #1 – Fibonacci-Folge
Eine Menge von „n“ Zahlen liegt in einer Fibonacci-Folge, wenn Zahl3=Zahl1+Zahl2, d. h. jede Zahl ist eine Summe ihrer beiden vorhergehenden Zahlen. Daher beginnt die Folge immer mit den ersten beiden Ziffern wie 0 und 1. Die dritte Ziffer ist eine Summe von 0 und 1, was zu 1 führt, die vierte Zahl ist die Addition von 1 und 1, was zu 2 führt, und die Folge geht weiter.
Schauen Sie sich den folgenden Code in Java an, um eine Fibonacci-Folge zu generieren:
Code:
public class FibonacciSeries{
static int num1=0,num2=1,num3=0;
static void fibonacci(int n){
if(n>0){
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
}
}
public static void main(String args[]){
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
}
}
Ausgabe:

Hier werden die ersten beiden Zahlen auf 0 und 1 initialisiert und gedruckt. Die Variablen „num1“, „num2“ und „num3“ werden verwendet, um die erforderliche Sequenz zu generieren. Die Variable „num3“ wird durch Addition von „num1“ und „num2“ erhalten, und die Zahlen werden durch Mischen um eine Position nach links verschoben, wie im Code gezeigt. Die Funktion „Fibonacci“ wird hier rekursiv aufgerufen und bei jeder Iteration wird der Wert von „n“ um 1 verringert. Daher wird die Rekursion beendet, sobald „n“ den Wert 0 erreicht.
Beispiel #2 – Turm von Hanoi
Dies ist ein klassisches mathematisches Problem, bei dem es drei Pole und eine „n“ Anzahl von Scheiben unterschiedlicher Größe gibt. Das Rätsel geht wie folgt:
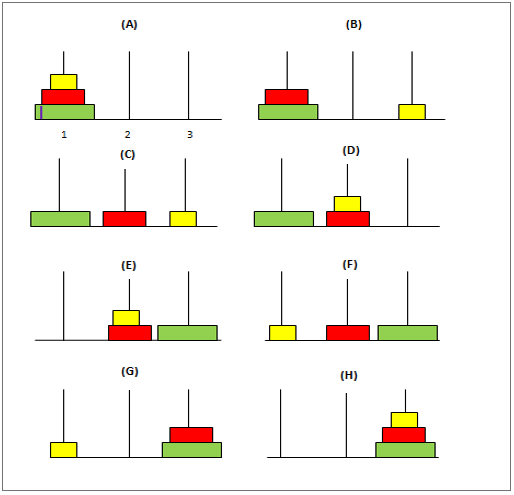
Am Anfang werden die Scheiben der ersten Stange so angeordnet sein, dass sich die größte Scheibe unten und die kleinste oben auf der Stange befindet. Das Ziel besteht darin, diese Scheiben vom ersten zum dritten Pol zu bewegen und dabei die gleiche Position wie im ersten Pol beizubehalten. Im Folgenden sind einige Bedingungen aufgeführt, die Sie beim Verschieben dieser Festplatten beachten sollten:
- Es muss jeweils nur eine Festplatte verschoben werden.
- Dabei ist es nicht erlaubt, eine größere Festplatte über eine kleinere zu legen.
- Der zweite (mittlere) Pol kann zur Vermittlung beim Übertragen der Bandscheiben vom ersten auf den zweiten Pol genutzt werden.
Folgend ist der Java-Code, der zum Lösen des Rätsels verwendet werden kann:
Code:
public class TowerOfHanoi {
public static void main(String[] args) {
int count = 3;
tower(count, 'A', 'B', 'C');
}
public static void tower(int first, char disk1, char temp, char disk2) {
if (first == 1) {
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
} else {
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
}
}
}
Ausgabe:
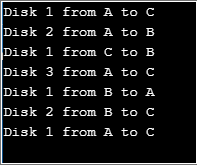
Here the variable “count” represents the number of discs to be used. The function “tower” is the recursive function used to move the discs from rod 1 to rod 3. A simple solution to this problem can be provided by considering 2 discs at first.
- First, we start by moving disc1 from rod 1 to rod 2.
- Next, we move disc2 to rod 3.
- Finally, we finish by moving disc1 to rod 3, completing the required solution.
This same principle is applied for the “n” number of discs by moving (n-1)the disc from rod 1 to 2 and following similar steps as above.
Example #3 – Factorial of Number
Code:
package com.recursion;
import java.util.Scanner;
public class FactorialOfNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Which number factorial do you want?=>");
//taking input from the user
int input = scanner.nextInt();
System.out.println("Factorial of " + input + "! is=>"+getMyFactorialNumber(input));
scanner.close();
}
public static long getMyFactorialNumber(int inputNumber) {
if (inputNumber == 1)//base condition
return 1;
return inputNumber * getMyFactorialNumber(inputNumber - 1);//recursive call
}
}
Output:
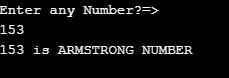
Example #4 – Armstrong Number
Code:
import java.util.Scanner;
//ARMSTRONG number means sum of numbers of cubes equal to the number
public class ArmstrongNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number?=>");
// taking input from the user
int input = scanner.nextInt();
//calling isArmstrongNumber() method and put in a variable
double checkNumber=isArmstrongNumber(input);
//checking the number
if(input==checkNumber)
{
System.out.println(input+" is ARMSTRONG NUMBER");
}
else
{
System.out.println(input+" not is ARMSTRONG NUMBER");
}
scanner.close();
}
static int remainderNumber;
static double total = 0;
public static double isArmstrongNumber(int inputNumber) {
if (inputNumber > 0) {
remainderNumber = inputNumber % 10;//separating digits
total = total + Math.pow(remainderNumber, 3);//cubes sum
isArmstrongNumber(inputNumber / 10);//recursive call
}
return total;
}
}
Output:
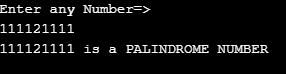
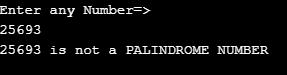
Example #5 – Palindrome Number
Code:
import java.util.Scanner;
public class PalindromeNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number=>");
// taking input from the user
int input = scanner.nextInt();
int checkNumber = palindromeNumberOrNot(input,0);
if (checkNumber == input)
{
System.out.println(input+" is a PALINDROME NUMBER");
}
else
{
System.out.println(input+" is not a PALINDROME NUMBER");
}
scanner.close();
}
public static int palindromeNumberOrNot(int inputNumber,int baseNumber) {
if (inputNumber == 0)// base case
return baseNumber;
baseNumber = (baseNumber * 10) + (inputNumber % 10);// getting the reverse of the number and stores in temp
return palindromeNumberOrNot(inputNumber/10,baseNumber);//recursive call
}
}
Output:
Conclusion
Recursive functions are relatively simpler to code, but they are also not that efficient as compared to the other existing methods. Hence they are majorly used in cases where the time given for development is less and also where a significant pattern can be observed in the problem.
Das obige ist der detaillierte Inhalt vonRekursion in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

