Pfad mit maximaler Wahrscheinlichkeit

1514. Pfad mit maximaler Wahrscheinlichkeit

Schwierigkeit:Mittel

Themen:Array, Graph, Heap (Prioritätswarteschlange), kürzester Pfad

Sie erhalten einen ungerichteten gewichteten Graphen von n Knoten (0-indiziert), dargestellt durch eine Kantenliste, wobei Kanten[i] = [a, b] eine ungerichtete Kante ist, die die Knoten a und b mit einer Erfolgswahrscheinlichkeit verbindet des Überquerens dieser Kante succProb[i].

Wenn zwei Knoten beginnen und enden, finden Sie den Pfad mit der maximalen Erfolgswahrscheinlichkeit von Anfang bis Ende und geben Sie seine Erfolgswahrscheinlichkeit zurück.

Wenn es keinen Pfad vom Anfang bis zum Ende gibt, geben Sie 0 zurück. Ihre Antwort wird akzeptiert, wenn sie um höchstens 1e-5.

von der richtigen Antwort abweicht

Beispiel 1:

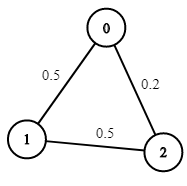
• Eingabe: n = 3, Kanten = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], Start = 0, Ende = 2
• Ausgabe: 0,25000
• Erklärung:Es gibt zwei Pfade von Anfang bis Ende, einer mit einer Erfolgswahrscheinlichkeit = 0,2 und der andere mit 0,5 * 0,5 = 0,25.

Beispiel 2:

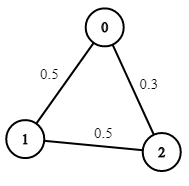
• Eingabe: n = 3, Kanten = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], Start = 0, Ende = 2
• Ausgabe: 0,30000

Beispiel 3:

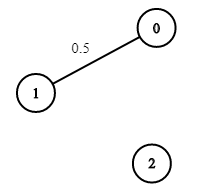
• Eingabe: n = 3, Kanten = [[0,1]], succProb = [0,5], Start = 0, Ende = 2
• Ausgabe: 0,00000
• Erklärung:Es gibt keinen Pfad zwischen 0 und 2.

Einschränkungen:

• 2 <= n <= 10^4
• 0 <= Anfang, Ende < n
• Anfang != Ende
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == Edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• Zwischen jeweils zwei Knoten liegt höchstens eine Kante

Hinweis:

1. Das Multiplizieren von Wahrscheinlichkeiten führt zu Präzisionsfehlern.
2. Verwenden Sie logarithmische Wahrscheinlichkeiten, um Zahlen zusammenzufassen, anstatt sie zu multiplizieren.
3. Verwenden Sie den Dijkstra-Algorithmus, um den minimalen Pfad zwischen den beiden Knoten zu finden, nachdem alle Kosten negiert wurden.

Lösung:

Wir können eine modifizierte Version des Dijkstra-Algorithmus verwenden. Anstatt den kürzesten Weg zu finden, maximieren Sie die Erfolgswahrscheinlichkeit.

Lassen Sie uns diese Lösung in PHP implementieren: 1514. Pfad mit maximaler Wahrscheinlichkeit

<?php
/**
 * @param Integer $n
 * @param Integer[][] $edges
 * @param Float[] $succProb
 * @param Integer $start_node
 * @param Integer $end_node
 * @return Float
 */
function maxProbability($n, $edges, $succProb, $start_node, $end_node) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example usage:
$n1 = 3;
$edges1 = [[0,1],[1,2],[0,2]];
$succProb1 = [0.5,0.5,0.2];
$start_node1 = 0;
$end_node1 = 2;

echo maxProbability($n1, $edges1, $succProb1, $start_node1, $end_node1);//Output: 0.25000


$n2 = 3;
$edges2 = [[0,1],[1,2],[0,2]];
$succProb2 = [0.5,0.5,0.3];
$start_node2 = 0;
$end_node2 = 2;

echo maxProbability($n2, $edges2, $succProb2, $start_node2, $end_node2);//Output: 0.30000


$n3 = 3;
$edges3 = [[0,1]];
$succProb3 = [0.5;
$start_node3 = 0;
$end_node3 = 2;

echo maxProbability($n3, $edges3, $succProb3, $start_node3, $end_node3); //Output: 0.00000
?>




<h3>
  
  
  Erläuterung:
</h3>

<ol>
<li><p><strong>Graphendarstellung</strong>: Der Graph wird als Adjazenzliste dargestellt, in der jeder Knoten auf seine Nachbarn zeigt, zusammen mit den Erfolgswahrscheinlichkeiten der sie verbindenden Kanten.</p></li>
<li><p><strong>Max Probability Array</strong>: Ein Array maxProb wird verwendet, um die maximale Wahrscheinlichkeit zu speichern, jeden Knoten vom Startknoten aus zu erreichen.</p></li>
<li><p><strong>Prioritätswarteschlange</strong>: Ein maximaler Heap (SplPriorityQueue) wird verwendet, um zuerst Pfade mit der höchsten Wahrscheinlichkeit zu erkunden. Dies ist entscheidend, um sicherzustellen, dass wir beim Erreichen des Zielknotens den Pfad mit der maximalen Wahrscheinlichkeit gefunden haben.</p></li>
<li>
<p><strong>Algorithmus</strong>:</p>

<ul>
<li>Initialisieren Sie die Wahrscheinlichkeit des Startknotens mit 1 (da die Wahrscheinlichkeit, am Start zu bleiben, 1 ist).</li>
<li>Verwenden Sie die Prioritätswarteschlange, um Knoten zu erkunden und die maximale Wahrscheinlichkeit, jeden Nachbarn zu erreichen, zu aktualisieren.</li>
<li>Wenn der Zielknoten erreicht ist, geben Sie die Wahrscheinlichkeit zurück.</li>
<li>Wenn kein Pfad vorhanden ist, geben Sie 0 zurück.</li>
</ul>
</li>
</ol>

<h3>
  
  
  Ausgabe:
</h3>

<p>Für das bereitgestellte Beispiel:<br>
</p>

<pre class="brush:php;toolbar:false">$n = 3;
$edges = [[0,1],[1,2],[0,2]];
$succProb = [0.5,0.5,0.2];
$start_node = 0;
$end_node = 2;

Die Ausgabe beträgt 0,25.

Dieser Ansatz gewährleistet eine effiziente Lösung unter Verwendung des Dijkstra-Algorithmus und berücksichtigt gleichzeitig die Besonderheiten von Wahrscheinlichkeitsberechnungen.

Kontaktlinks

Wenn Sie diese Serie hilfreich fanden, denken Sie bitte darüber nach, dem Repository einen Stern auf GitHub zu geben oder den Beitrag in Ihren bevorzugten sozialen Netzwerken zu teilen? Ihre Unterstützung würde mir sehr viel bedeuten!

Wenn Sie weitere hilfreiche Inhalte wie diesen wünschen, folgen Sie mir gerne:

• LinkedIn
• GitHub

Das obige ist der detaillierte Inhalt vonPfad mit maximaler Wahrscheinlichkeit. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!