Heim >Backend-Entwicklung >PHP-Tutorial >Maximale Punktzahl mit Kosten
Maximale Punktzahl mit Kosten
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2024-08-18 06:46:021072Durchsuche
1937. Maximale Punktzahl mit Kosten
Schwierigkeit:Mittel
Themen:Array, dynamische Programmierung
Sie erhalten m x n ganzzahlige Matrixpunkte (0-indiziert). Beginnend mit 0 Punkten möchten Sie die Anzahl der Punkte, die Sie aus der Matrix erhalten können, maximieren.
Um Punkte zu sammeln, müssen Sie in jeder Zeile eine Zelle auswählen. Wenn Sie die Zelle bei den Koordinaten (r, c) auswählen, werden Punkte[r][c] zu Ihrer Punktzahl hinzugefügt.
Sie verlieren jedoch Punkte, wenn Sie eine Zelle auswählen, die zu weit von der Zelle entfernt ist, die Sie in der vorherigen Zeile ausgewählt haben. Für alle zwei benachbarten Zeilen r und r + 1 (wobei 0 <= r < m - 1) Zellen an den Koordinaten (r, c1) und (r + 1, c auswählen 2) subtrahiert abs(c1 - c2) von Ihrer Punktzahl.
Geben Siedie maximale Anzahl an Punkten zurück, die Sie erreichen können.
abs(x) ist definiert als:
-
x für x >= 0.
- -x für x < 0.
Beispiel 1:
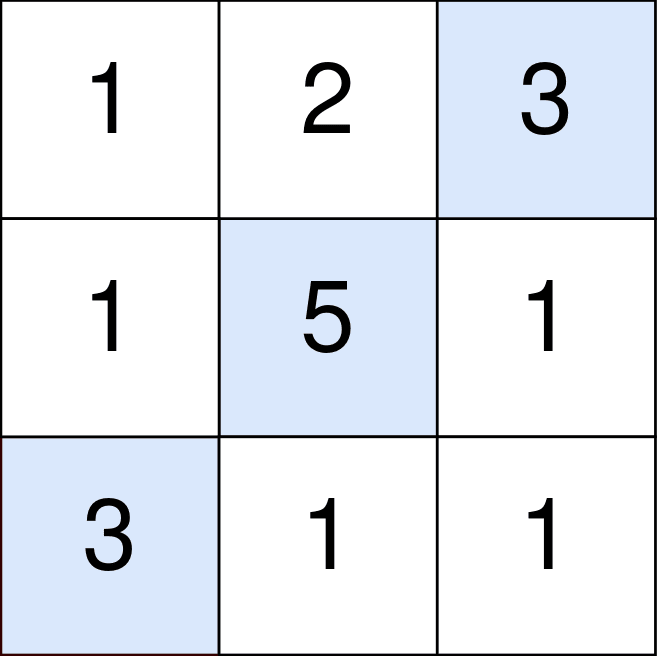
- Eingabe: l1 = [2,4,3], l2 = [5,6,4]
- Ausgabe: 9
- Erklärung:
- Die blauen Zellen stellen die optimal auszuwählenden Zellen dar, die die Koordinaten (0, 2), (1, 1) und (2, 0) haben.
- Sie addieren 3 + 5 + 3 = 11 zu Ihrer Punktzahl.
- Sie müssen jedoch abs(2 - 1) + abs(1 - 0) = 2 von Ihrer Punktzahl abziehen.
- Ihr Endergebnis ist 11 - 2 = 9.
Beispiel 2:
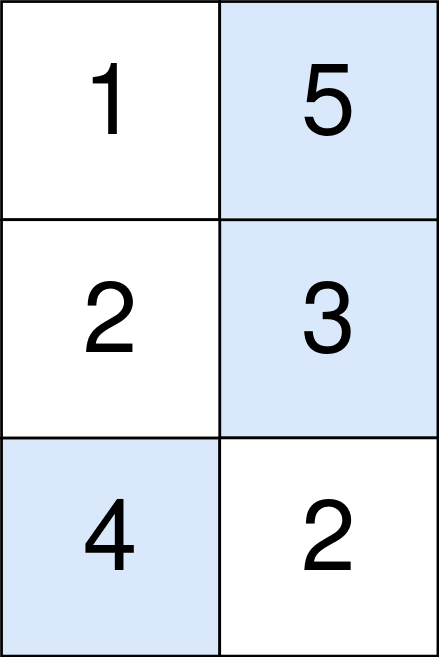
- Eingabe: Punkte = [[1,5],[2,3],[4,2]]
- Ausgabe: 11
- Erklärung:
- Die blauen Zellen stellen die optimal auszuwählenden Zellen dar, die die Koordinaten (0, 1), (1, 1) und (2, 0) haben.
- Sie addieren 5 + 3 + 4 = 12 zu Ihrer Punktzahl.
- Sie müssen jedoch abs(1 - 1) + abs(1 - 0) = 1 von Ihrer Punktzahl abziehen.
- Ihr Endergebnis ist 12 - 1 = 11.
Einschränkungen:
- m == Punkte.Länge
- n == Punkte[r].Länge
- 1 <= m, n <= 10
- 5 1 <= m * n <= 10
- 5 0 <= Punkte[r][c] <= 10
- 5
Hinweis:
- Versuchen Sie es mit dynamischer Programmierung.
- dp[i][j] ist die maximale Anzahl von Punkten, die Sie haben können, wenn Punkte[i][j] die zuletzt ausgewählte Zelle ist.
Lösung:
Wir können die Lösung in mehrere Schritte unterteilen:Schritt 1: Definieren Sie das DP-Array
Wir verwenden ein 2D-Array dp, wobei dp[i][j] die maximale Punktzahl darstellt, die wir durch Auswahl der Zelle in Zeile i und Spalte j erreichen können.
Schritt 2: Initialisieren Sie das DP-Array
Initialisieren Sie die erste Reihe von dp so, dass sie mit der ersten Reihe von Punkten übereinstimmt, da es keine vorherigen Reihen gibt, um die Kosten zu subtrahieren.
Schritt 3: Berechnen Sie die DP-Werte für jede Zeile
Für jede weitere Zeile berechnen wir die maximal möglichen Punkte für jede Spalte unter Berücksichtigung der Kosten für den Wechsel von der vorherigen Zeile.
Um den Übergang von Zeile i-1 zu Zeile i effizient zu berechnen, können wir links und rechts zwei Hilfsarrays verwenden:
-
left[j] speichert den Maximalwert, den wir für die j-te Spalte erreichen können, wobei nur Übergänge von links berücksichtigt werden.
- right[j] speichert den Maximalwert, den wir für die j-te Spalte erreichen können, wobei nur Übergänge von rechts berücksichtigt werden.
Für jede Spalte j in Zeile i:
- Aktualisieren Sie dp[i][j] mit dem Maximum von links[j] oder rechts[j] plus Punkten[i][j].
Das Ergebnis ist der Maximalwert in der letzten Zeile des dp-Arrays.
Lassen Sie uns diese Lösung in PHP implementieren:
1937. Maximale Punktzahl mit Kosten
Erläuterung:
- linke und rechte Arrays: Diese helfen uns bei der Berechnung der maximalen Punkte, die wir für jede Zelle gewinnen können, indem wir die Werte der vorherigen Zeile berücksichtigen und so den Nachteil effizient berücksichtigen, der durch das Verschieben über Spalten hinweg entsteht.
- Dynamischer Programmieransatz:Diese Methode stellt sicher, dass jede Zeile auf der Grundlage der vorherigen Zeile berechnet wird, wodurch die Lösung für große Matrizen skalierbar wird.
Kontaktlinks
Wenn Sie diese Serie hilfreich fanden, denken Sie bitte darüber nach, dem Repository einen Stern auf GitHub zu geben oder den Beitrag in Ihren bevorzugten sozialen Netzwerken zu teilen? Ihre Unterstützung würde mir sehr viel bedeuten!
Wenn Sie weitere hilfreiche Inhalte wie diesen wünschen, folgen Sie mir gerne:
- GitHub
Das obige ist der detaillierte Inhalt vonMaximale Punktzahl mit Kosten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- So verwenden Sie cURL zum Implementieren von Get- und Post-Anfragen in PHP
- So verwenden Sie cURL zum Implementieren von Get- und Post-Anfragen in PHP
- So verwenden Sie cURL zum Implementieren von Get- und Post-Anfragen in PHP
- So verwenden Sie cURL zum Implementieren von Get- und Post-Anfragen in PHP
- Alle Ausdruckssymbole in regulären Ausdrücken (Zusammenfassung)

