Max-Subarray-Problem und Kadanes Algorithmus

Das Max-Subarray-Problem und seine Geschichte

In den späten 1970er Jahren diskutierte der schwedische Mathematiker Ulf Grenander ein Problem: Wie kann man ein 2D-Array von Bilddaten effizienter analysieren als mit roher Gewalt? Damals waren die Computer langsam und die Bilder im Verhältnis zum Arbeitsspeicher groß. Um die Sache noch schlimmer zu machen, benötigte rohe Gewalt im schlimmsten Fall O(n^6) Zeit (sextische Zeitkomplexität).

Zuerst vereinfachte Grenandier die Frage: Wie würden Sie bei einem nur eindimensionalen Zahlenarray am effizientesten das zusammenhängende Unterarray mit der größten Summe finden?

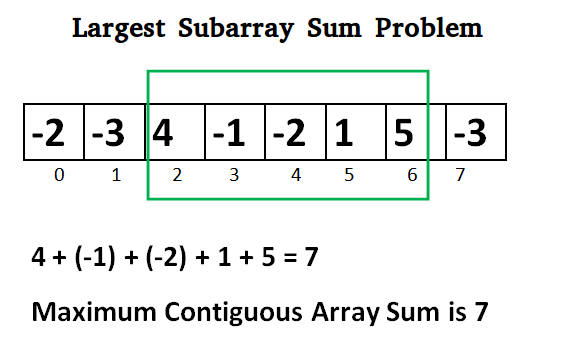
Brute Force: Ein naiver Ansatz mit kubischer Zeitkomplexität

Brute Gewalt würde die Analyse eines 1D-Arrays halb so lange dauern wie die eines 2D-Arrays, also O(n^3), um jede mögliche Kombination zu untersuchen (kubische Zeitkomplexität).

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j+1]
            for k in range(i, j + 1):
                current_sum += arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Grenanders O(n²)-Optimierung: Ein Schritt vorwärts

Grenander hat es auf eine O(n^2)-Lösung verbessert. Ich konnte seinen Code bei meiner Recherche nicht finden, aber ich vermute, dass er einfach die innerste Schleife entfernt hat, die alle Zahlen zwischen den beiden Indizes addiert. Stattdessen können wir beim Durchlaufen des Subarrays eine laufende Summe beibehalten und so die Anzahl der Schleifen von drei auf zwei reduzieren.

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum += arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

Shamos' Divide and Conquer: Aufteilung des Problems für O(n log n)

Grenander zeigte dem Informatiker Michael Shamos das Problem. Shamos dachte eine Nacht lang darüber nach und entwickelte eine Teile-und-Herrsche-Methode, die O(n log n) ist.

Es ist ziemlich clever. Die Idee besteht darin, das Array in zwei Hälften zu teilen und dann rekursiv die maximale Subarray-Summe für jede Hälfte sowie das Subarray zu ermitteln, das den Mittelpunkt kreuzt.

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum += arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid + 1, right + 1):
        current_sum += arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum + right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left + right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid + 1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Dies reduziert die zeitliche Komplexität auf O(nlogn)-Zeit, da zuerst das Array in zwei Hälften geteilt wird (O(logn)) und dann das Finden des maximal kreuzenden Subarrays O(n) benötigt

Kadanes Algorithmus: Die elegante O(n)-Lösung

Der Statistiker Jay Kadane hat sich den Code angesehen und sofort festgestellt, dass die Lösung von Shamos die Kontiguitätsbeschränkung nicht als Teil der Lösung verwendet.

Das ist ihm klar geworden

-Wenn ein Array nur negative Zahlen enthält, ist die Antwort immer die größte einzelne Zahl im Array, vorausgesetzt, wir lassen keine leeren Unterarrays zu.

-Wenn ein Array nur positive Zahlen enthält, besteht die Antwort immer darin, das gesamte Array zu addieren.

-Wenn Sie ein Array mit sowohl positiven als auch negativen Zahlen haben, können Sie das Array Schritt für Schritt durchlaufen. Wenn die Zahl, die Sie betrachten, zu irgendeinem Zeitpunkt größer ist als die Summe aller Zahlen davor, kann die Lösung keine der vorherigen Zahlen enthalten. Somit beginnen Sie eine neue Summe ab der aktuellen Zahl und behalten dabei den Überblick über die bisher erreichte Höchstsumme.

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum + num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

Was ich an diesem Algorithmus liebe, ist, dass er auf viele andere Probleme angewendet werden kann. Versuchen Sie es anzupassen, um diese LeetCode-Probleme zu lösen:

Einsen und Nullen
Maximalsummen-Zirkular-Subarray
Subarray-Summe mit minimaler Größe
Maximale aufsteigende Subarray-Summe
Maximales Produkt-Subarray
Kontinuierliche Subarray-Summe
Maximales Wechselsummen-Subarray (Premium)
Maximale Summe des Rechtecks ​​nicht größer als K

Das obige ist der detaillierte Inhalt vonMax-Subarray-Problem und Kadanes Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!