Heim >Hardware-Tutorial >Hardware-Rezension >Tsinghua Optics AI erscheint in der Natur! Physisches neuronales Netzwerk, Backpropagation ist nicht mehr erforderlich
Tsinghua Optics AI erscheint in der Natur! Physisches neuronales Netzwerk, Backpropagation ist nicht mehr erforderlich
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2024-08-10 22:15:061282Durchsuche
Die Ergebnisse der Tsinghua-Universität mithilfe von Licht zum Trainieren neuronaler Netze wurden kürzlich in Nature veröffentlicht!
Was soll ich tun, wenn der Backpropagation-Algorithmus nicht angewendet werden kann?
Sie schlugen eine Trainingsmethode im Fully Forward Mode (FFM) vor, die den Trainingsprozess direkt im physischen optischen System durchführt und so die Einschränkungen herkömmlicher digitaler Computersimulationen überwindet.

Vereinfacht ausgedrückt war es früher notwendig, das physikalische System im Detail zu modellieren und diese Modelle dann am Computer zu simulieren, um das Netzwerk zu trainieren. Die FFM-Methode eliminiert den Modellierungsprozess und ermöglicht es dem System, experimentelle Daten direkt zum Lernen und zur Optimierung zu nutzen.
Dies bedeutet auch, dass beim Training nicht mehr jede Schicht von hinten nach vorne überprüft werden muss (Backpropagation), sondern die Parameter des Netzwerks direkt von vorne nach hinten aktualisiert werden können.
Zum Beispiel muss die Backpropagation, genau wie ein Puzzle, zuerst das endgültige Bild (Ausgabe) sehen und es dann Stück für Stück in umgekehrter Reihenfolge überprüfen und wiederherstellen, während die FFM-Methode eher einem teilweise abgeschlossenen Puzzle in der Hand ähnelt muss einigen leichten Prinzipien folgen (symmetrische Reziprozität). Füllen Sie weiter aus, ohne die vorherigen Puzzleteile noch einmal zu überprüfen.

Auf diese Weise liegen auch die Vorteile der Verwendung von FFM auf der Hand:
Erstens wird die Abhängigkeit von mathematischen Modellen verringert, wodurch Probleme durch ungenaue Modelle vermieden werden können. Zweitens wird Zeit gespart (und weniger Energie verbraucht). Durch den Einsatz optischer Systeme können große Datenmengen und Vorgänge parallel verarbeitet werden. Durch die Eliminierung der Backpropagation verringert sich auch die Anzahl der Schritte im gesamten Netzwerk, die überprüft und angepasst werden müssen.
Die Co-Autoren des Papiers sind Xue Zhiwei und Zhou Tiankui von der Tsinghua-Universität, und die entsprechenden Autoren sind Professor Fang Lu und Akademiker Dai Qionghai von der Tsinghua-Universität. Darüber hinaus beteiligten sich auch Xu Zhihao vom Fachbereich Elektronik der Tsinghua-Universität und Yu Shaoliang vom Zhijiang-Labor an dieser Forschung.
Rückausbreitung eliminieren
Zusammenfassung des FFM-Prinzips in einem Satz:
Ordnen Sie das optische System einem parametrisierten neuronalen Netzwerk vor Ort zu, berechnen Sie den Gradienten durch Messung des Ausgangslichtfelds und aktualisieren Sie die Parameter mithilfe des Gradientenabstiegsalgorithmus.
Einfach ausgedrückt bedeutet es, das optische System sich selbst beibringen zu lassen, seine eigene Leistung zu verstehen, indem man beobachtet, wie es Licht verarbeitet (d. h. das Ausgangslichtfeld misst), und diese Informationen dann zu verwenden, um seine Einstellungen (Parameter) schrittweise anzupassen.
Die folgende Abbildung zeigt den Funktionsmechanismus von FFM in einem optischen System:
wobei a die Einschränkung der traditionellen Entwurfsmethode ist; b die Zusammensetzung des optischen Systems ist; c die Abbildung des optischen Systems auf das neuronale Netzwerk .

Erweitert besteht das allgemeine optische System (b), einschließlich Freiraumlinsenoptik und integrierter Photonik, aus einem Modulationsbereich (dunkelgrün) und einem Ausbreitungsbereich (hellgrün). In diesen Bereichen ist der Brechungsindex des Modulationsbereichs einstellbar, während der Brechungsindex des Ausbreitungsbereichs fest ist.
Und die Modulations- und Ausbreitungsbereiche können hier auf die Gewichte und Neuronenverbindungen im neuronalen Netzwerk abgebildet werden.
In einem neuronalen Netzwerk sind diese verstellbaren Teile wie Verbindungspunkte zwischen Neuronen und können ihre Stärke (Gewichte) ändern, um zu lernen.
Unter Verwendung des Prinzips der Reziprozität der räumlichen Symmetrie können Daten und Fehlerberechnung denselben physikalischen Vorwärtsausbreitungsprozess und dieselbe Messmethode verwenden.
Es ist ein bisschen wie eine Spiegelung, jeder Teil des Systems reagiert auf Lichtausbreitung und Fehlerrückmeldungen auf die gleiche Weise. Das bedeutet, dass das System unabhängig davon, wie viel Licht in das System eindringt, es konsistent verarbeitet und sich anhand der Ergebnisse anpasst.
Auf diese Weise kann der Gradient direkt vor Ort berechnet und zur Aktualisierung des Brechungsindex innerhalb des Designbereichs verwendet werden, wodurch die Systemleistung optimiert wird.
Durch die Gradientenabstiegsmethode vor Ort kann das optische System seine Parameter schrittweise anpassen, bis es den optimalen Zustand erreicht.
Der Originaltext verwendet die Gleichung, um schließlich die oben erwähnte Gradientenabstiegsmethode im vollständigen Vorwärtsmodus (anstelle der Rückausbreitung) auszudrücken als:
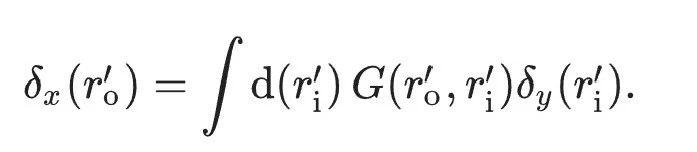
Eine Trainingsmethode für optische neuronale Netze
Als Trainingsmethode für optische neuronale Netze, FFM Es hat folgende Vorteile:
Genauigkeit vergleichbar mit dem idealen Modell
Mit FFM kann ein effektiver Selbsttrainingsprozess im optischen neuronalen Freiraumnetz (ONN) erreicht werden.

Um diese Schlussfolgerung zu veranschaulichen, verwendeten die Forscher zunächst ein einschichtiges ONN, um ein Objektklassifizierungstraining für den Benchmark-Datensatz durchzuführen (a).
Konkret verwendeten sie einige Bilder handgeschriebener Ziffern (MNIST-Datensatz), um dieses System zu trainieren, und visualisierten dann die Ergebnisse (b).
Die Ergebnisse zeigen, dass das durch FFM-Lernen trainierte ONN eine extrem hohe Ähnlichkeit zwischen dem experimentellen Lichtfeld und dem theoretischen Lichtfeld aufweist (SSIM übersteigt 0,97).
Mit anderen Worten: Es lernt so gut, dass es die ihm gegebenen Beispiele nahezu perfekt nachahmen kann.
Dennoch erinnern Forscher auch daran:
Aufgrund von Unvollkommenheiten im System können die theoretisch berechneten Lichtfelder und -gradienten tatsächliche physikalische Phänomene nicht vollständig genau widerspiegeln.
Als nächstes verwendeten die Forscher komplexere Bilder (Fashion-MNIST-Datensatz), um das System darauf zu trainieren, verschiedene Modeartikel zu erkennen.
Zu Beginn, als die Anzahl der Schichten von 2 auf 8 stieg, betrug die durchschnittliche Genauigkeit des computertrainierten Netzwerks fast die Hälfte der theoretischen Genauigkeit.
Mit der FFM-Lernmethode wurde die Netzwerkgenauigkeit des Systems auf 92,5 % erhöht, was nahe am theoretischen Wert liegt.
Dies zeigt, dass mit zunehmender Anzahl der Netzwerkschichten die Leistung des mit herkömmlichen Methoden trainierten Netzwerks abnimmt, während FFM-Lernen eine hohe Genauigkeit aufrechterhalten kann.
Gleichzeitig kann die Leistung von ONN durch die Einbeziehung nichtlinearer Aktivierung in das FFM-Lernen weiter verbessert werden. In Experimenten konnte durch nichtlineares FFM-Lernen die Klassifizierungsgenauigkeit von 90,4 % auf 93,0 % verbessert werden.
Untersuchungen belegen außerdem, dass durch Batch-Training nichtlinearer ONN der Fehlerausbreitungsprozess vereinfacht werden kann und sich die Trainingszeit nur um das 1- bis 1,7-fache erhöht.
Fähigkeit zur hochauflösenden Fokussierung
FFM kann auch in praktischen Anwendungen eine qualitativ hochwertige Bildgebung erzielen und selbst in komplexen Streuumgebungen eine Auflösung nahe der physikalischen Grenze erreichen.
Wenn Lichtwellen in ein Streumedium (wie Nebel, Rauch oder biologisches Gewebe usw.) eindringen, wird die Fokussierung zunächst kompliziert, aber die Ausbreitung von Lichtwellen im Medium behält oft eine gewisse Symmetrie bei.
FFM nutzt diese Symmetrie, indem es den Ausbreitungsweg und die Phase von Lichtwellen optimiert, um die negativen Auswirkungen von Streueffekten auf die Fokussierung zu reduzieren.
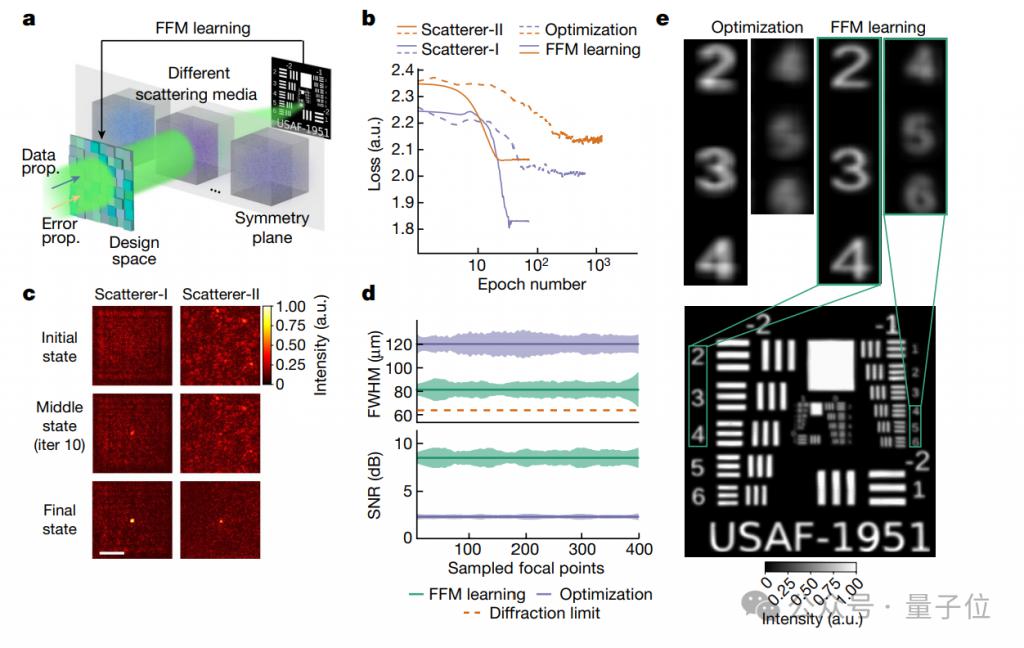
Der Effekt ist auch sehr signifikant. Abbildung b zeigt den Vergleich der beiden Optimierungsverfahren FFM und PSO (Particle Swarm Optimization).
Konkret wurden bei dem Experiment zwei Streumedien verwendet, eines ist eine Zufallsphasenplatte (Scatterer-I) und das andere ein transparentes Band (Scatterer-II).
In beiden Medien erreichte FFM Konvergenz (schnelleres Finden der optimalen Lösung) nach nur 25 Entwurfsiterationen mit Konvergenzverlustwerten von 1,84 bzw. 2,07 (niedriger bedeutet bessere Leistung).
Die PSO-Methode erfordert mindestens 400 Entwurfsiterationen, um Konvergenz zu erreichen, und die Verlustwerte bei endgültiger Konvergenz betragen 2,01 und 2,15.
Gleichzeitig zeigt Abbildung c, dass FFM in der Lage ist, sich kontinuierlich zu optimieren, und dass sich der Fokus schrittweise weiterentwickelt und von einer anfänglichen Zufallsverteilung zu einem engen Fokus konvergiert.
Innerhalb einer Entwurfsfläche von 3,2 mm × 3,2 mm haben die Forscher die FFM- und PSO-optimierten Brennpunkte weiter gleichmäßig abgetastet und deren FWHM (Vollbreite bei halbem Maximum) und PSNR (Spitzensignal-Rausch-Verhältnis) verglichen.
Die Ergebnisse zeigen, dass FFM eine höhere Fokussierungsgenauigkeit und eine bessere Bildqualität aufweist.
Abbildung e bewertet weiter die Leistung des entworfenen Fokusarrays beim Scannen einer Auflösungskarte, die sich hinter einem Streumedium befindet.
Die Ergebnisse sind überraschend. Die Fokusgröße des FFM-Designs liegt nahe an der Beugungsgrenze von 64,5 m, dem theoretisch höchsten Auflösungsstandard für die optische Bildgebung.
Kann parallel Objekte außerhalb der Sichtlinie abbilden
Da es bei der Streuung von Medien so leistungsstark ist, haben die Forscher auch Szenarien ohne Sichtlinie (NLOS) ausprobiert, bei denen Objekte außerhalb der Sichtlinie verborgen sind.

FFM nutzt die räumliche Symmetrie des Lichtwegs vom versteckten Objekt zum Beobachter aus, wodurch das System dynamische versteckte Objekte im Feld auf rein optische Weise rekonstruieren und analysieren kann.
Durch die Gestaltung der Eingangswellenfront ist FFM in der Lage, alle Netze im Objekt gleichzeitig an ihre Zielpositionen zu projizieren und so eine parallele Wiederherstellung versteckter Objekte zu erreichen.
Die buchstabenförmigen versteckten Chrom-Targets „T“, „H“ und „U“ wurden im Experiment verwendet und die Belichtungszeit (1 Millisekunde) und die optische Leistung (0,20 mW) wurden so eingestellt, dass eine schnelle Abbildung dieser Dynamik erreicht wird Ziele.
Die Ergebnisse zeigen, dass das Bild ohne die von FFM entworfene Wellenfront stark verzerrt sein wird. Während die von FFM entworfene Wellenfront die Formen aller drei Buchstaben wiederherstellen konnte, erreichte der SSIM (struktureller Ähnlichkeitsindex) 1,0, was auf einen hohen Grad an Ähnlichkeit mit dem Originalbild hinweist.
Darüber hinaus übertrifft FFM im Vergleich zu künstlichen neuronalen Netzwerken (KNN) in Bezug auf Photoneneffizienz und Klassifizierungsleistung KNN erheblich, insbesondere unter Bedingungen mit geringen Photonen.
Insbesondere in Situationen, in denen die Anzahl der Photonen begrenzt ist (z. B. bei vielen reflektierenden oder stark diffusen Oberflächen), ist FFM in der Lage, Wellenfrontverzerrungen adaptiv zu korrigieren und benötigt weniger Photonen für eine genaue Klassifizierung.
Automatische Suche nach Ausreißern in nicht-hermiteschen Systemen
FFM-Methoden sind nicht nur auf optische Freiraumsysteme anwendbar, sondern können auch auf den Selbstentwurf integrierter photonischer Systeme erweitert werden.

Die Forscher konstruierten ein integriertes neuronales Netzwerk (a) unter Verwendung symmetrischer photonischer Kerne, die in Reihe und parallel konfiguriert sind.
Im Experiment wurde der symmetrische Kern mit einem variablen optischen Dämpfer (VOA) durch unterschiedliche Injektionsstromstärken konfiguriert, um unterschiedliche Dämpfungskoeffizienten zu erreichen und unterschiedliche Gewichte zu simulieren.
그림 c에서 대칭 코어에 프로그래밍된 행렬 값의 충실도는 매우 높으며 시간 드리프트의 표준 편차는 각각 0.012%, 0.012% 및 0.010%로 행렬 값이 매우 안정적임을 나타냅니다.
그리고 연구원들은 각 레이어의 오류를 시각화했습니다. 실험적 변화도를 이론적 시뮬레이션 값과 비교하면 평균 편차는 3.5%입니다.
약 100번의 반복(에포크) 후에 네트워크는 수렴에 도달합니다.
실험 결과에 따르면 세 가지 다른 대칭 비율 구성(1.0, 0.75 또는 0.5)에서 네트워크의 분류 정확도는 각각 94.7%, 89.2% 및 89.0%입니다.
FFM 방식을 이용한 신경망을 이용하여 얻은 분류 정확도는 94.2%, 89.2%, 88.7%입니다.
반대로 전통적인 컴퓨터 시뮬레이션 방법을 사용하여 네트워크를 설계하는 경우 실험의 분류 정확도는 각각 71.7%, 65.8% 및 55.0%로 낮아집니다.
마지막으로 연구원들은 FFM이 비 에르미트 시스템을 자체 설계하고 수치 시뮬레이션을 통해 물리적 모델 없이도 특이점 통과를 달성할 수 있음을 입증했습니다.
비에르미트 시스템(Non-Hermitian system)은 물리학의 개념으로, 에르미트 조건을 만족하지 않는 양자역학, 광학 등 분야의 시스템을 포함합니다.
Hermitian 속성은 시스템의 대칭 및 실제 에너지 수와 관련이 있습니다. Non-Hermitian 시스템은 이러한 조건을 충족하지 않으며 역학인 예외점(Exceptional Point)과 같은 특별한 물리적 현상을 가질 수 있습니다. 학습 행동이 특정 지점에서 이상한 변화를 겪는 곳입니다.
전체 기사를 요약하면 FFM은 대부분의 기계 학습 작업을 병렬로 효율적으로 실행할 수 있는 물리적 시스템에 계산 집약적인 훈련 프로세스를 구현하는 방법입니다.
자세한 실험 설정 및 데이터 세트 준비 과정은 원문을 참고해주세요.
코드:
https://zenodo.org/records/10820584
"자연"의 원본 텍스트:
https://www.nature.com/articles/s41586-024-07687-4
Das obige ist der detaillierte Inhalt vonTsinghua Optics AI erscheint in der Natur! Physisches neuronales Netzwerk, Backpropagation ist nicht mehr erforderlich. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Der Groll von Ni Shuihans intelligentem NPC bereitet mir ein schlechtes Gewissen ...
- Tatsächliche Messung der Signalstärke im Vergleich zwischen iPhone 15 und Mate60P, Ergebnisse enthüllt
- Huawei Mate 60 Pro-Signaltest: Es gibt Bedauern, aber es gibt noch mehr Überraschungen
- Schätzen Sie den facettenreichen Charme von Aichir Time Elf: sowohl frisch und smart als auch smart und multifunktional
- Tatsächliche Testergebnisse von Huawei-Satellitenanrufen: Die Klangqualität übertrifft die professioneller Satellitentelefone

