Heim >Web-Frontend >js-Tutorial >Finanzielle Präzision in JavaScript: Mit Geld umgehen, ohne einen Cent zu verlieren
Finanzielle Präzision in JavaScript: Mit Geld umgehen, ohne einen Cent zu verlieren
- WBOYOriginal
- 2024-08-10 06:45:02890Durchsuche

In der schnelllebigen Finanzwelt ist Präzision alles. Es ist immer besser, einen Millionenverlust aufgrund eines Rundungs-/Präzisionsfehlers zu vermeiden.
Wenn es um Geld geht, denken Sie an den Datentyp
Der Ausgangspunkt dieses Artikels ist die Erkenntnis, dass Geld nicht die durchschnittliche Grundzahl ist, mit der Sie die Äpfel in Ihrem Warenkorb zählen können. Was erhalten Sie, wenn Sie versuchen, 10 € mit 10 $ zu multiplizieren? Schwierig, oder? Haben Sie schon einmal wundersame 1.546 $ in der Tasche einer alten Jacke gefunden? Ja, ich weiß, das ist auch nicht wirklich möglich. Diese albernen Beispiele sollen die Tatsache veranschaulichen, dass Geld seine eigenen Regeln hat und nicht nur durch eine einfache Zahl modelliert werden kann. Ich versichere Ihnen, ich bin nicht der Erste, der das erkannt hat (und vielleicht haben Sie es schon viel vor mir erkannt). Im Jahr 2002 schlug der Programmierer Martin Fowler in den Patterns of Enterprise Application Architecture eine Möglichkeit vor, Geld mit spezifischen Attributen und Operandenregeln darzustellen. Für ihn waren die beiden minimal brauchbaren Attribute, die für einen Gelddatentyp benötigt wurden:
amount currency
Diese wirklich grundlegende Darstellung wird unser Ausgangspunkt für die Konstruktion eines einfachen, aber robusten Geldmodells sein.
Geldbeträge, wie man sie darstellt
Ein Geldbetrag ist definitiv eine bestimmte Zahl: Sie hat eine feste Genauigkeit (auch hier können Sie nicht 4,376 $ in Ihrer Tasche haben). Sie müssen eine Art der Darstellung wählen, die Ihnen hilft, diese Einschränkung zu respektieren.
Ein naiver Ansatz, der native Zahlen-JavaScript-Datentyp
Spoiler-Alarm, das ist definitiv keine gute Idee, wenn Sie nicht wollen, dass ein paar Cent (wenn es nicht Dollar sind) in der dunklen Welt der Gleitkommazahlendarstellung verschwinden.
Der kostspielige Präzisionsfehler
Wenn Sie Erfahrung mit dem Codieren in JavaScript haben, wissen Sie, dass selbst die einfachste Berechnung zu einem Präzisionsfehler führen kann, den Sie zunächst nicht erwarten würden. Das offensichtlichste und bekannteste Beispiel, das dieses Phänomen verdeutlicht, ist:
0.1 + 0.2 !== 0.3 // true 0.1 + 0.2 // 0.30000000000000004
Wenn Sie dieses Beispiel nicht vollständig überzeugt, empfehle ich Ihnen, einen Blick auf diesen Artikel zu werfen, der sich etwas eingehender mit allen problematischen Berechnungsergebnissen befasst, die bei der Arbeit mit dem nativen JavaScript-Zahlentyp auftreten können …
Diese leichte Abweichung in den Ergebnissen mag für Sie harmlos erscheinen (mit einer Größenordnung von etwa ~ 10^-16), in einer kritischen Finanzanwendung kann sich ein solcher Fehler jedoch schnell ausbreiten. Erwägen Sie den Transfer von Geldern zwischen Tausenden von Konten, wobei jede Transaktion ähnliche Berechnungen erfordert. Die geringfügigen Ungenauigkeiten summieren sich und bevor Sie es merken, sind Ihre Finanzberichte um Tausende von Dollar falsch. Und ehrlich gesagt sind wir uns alle einig, dass Fehler nicht erlaubt sind, wenn es um Geld geht: sowohl rechtlich als auch um eine vertrauensvolle Beziehung zu Ihren Kunden aufzubauen.
Warum so ein Fehler?
Die erste Frage, die ich mir stellte, als ich in einem meiner Projekte auf das Problem stieß, war Warum ? Ich habe herausgefunden, dass die Ursache des Problems nicht JavaScript ist und dass diese Ungenauigkeiten auch andere moderne Programmiersprachen (Java, C, Python, …) betreffen.
// In C
#include <stdio.h>
int main() {
double a = 0.1;
double b = 0.2;
double sum = a + b;
if (sum == 0.3) {
printf("Equal\n");
} else {
printf("Not Equal\n"); // This block is executed
}
return 0;
}
// > Not equal
// In Java
public class doublePrecision {
public static void main(String[] args) {
double total = 0;
total += 5.6;
total += 5.8;
System.out.println(total);
}
}
// > 11.399999999999
Tatsächlich liegt die Ursache im Standard, den diese Sprachen zur Darstellung von Gleitkommazahlen verwenden: dem Gleitkommaformat mit doppelter (oder einfacher) Genauigkeit, das durch den IEEE 754-Standard spezifiziert wird.
IEEE 754-Standard: eine Geschichte der Bitdarstellung
In Javascript entspricht der native Typ Zahl Gleitkommazahlen mit doppelter Genauigkeit, was bedeutet, dass eine Zahl mit 64 Bit codiert und in drei Teile unterteilt wird:
- 1 Bit für das Vorzeichen
- 11 Bits für den Exponenten
- 52 Bits für die Mantisse (oder den Bruch), die von 0 bis 1 reicht
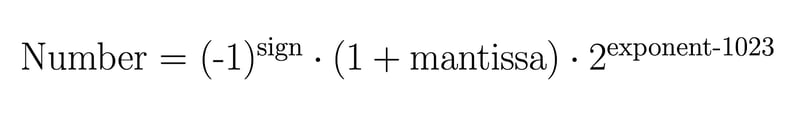
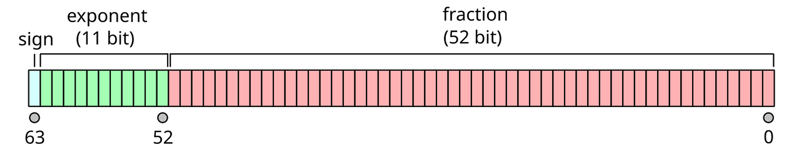
Dann müssen Sie die folgende Formel verwenden, um Ihre Bitdarstellung in einen Dezimalwert umzuwandeln:
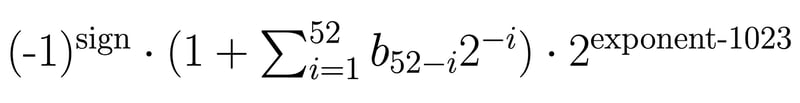
Ein Beispiel für die Darstellung von Gleitkommazahlen mit doppelter Genauigkeit, eine Näherung von 1/3 :
0 01111111101 0101010101010101010101010101010101010101010101010101 = (-1)^0 x (1 + 2^-2 + 2^-4 + 2^-6 + ... + 2^-50 + 2^-52) x 2^(1021-1023) = 0.333333333333333314829616256247390992939472198486328125 ~ 1/3
This format allows us to represent a vast range of values, but it can't represent every possible number with absolute precision (just between 0 and 1 you can find an infinity of numbers…). Many numbers cannot be represented exactly in binary form. To loop on the first example, that's the issue with 0.1 and 0.2. Double-point floating representation gives us an approximation of these value, so when you add these two imprecise representations, the result is also not exact.
A possible solution: Arbitrary Decimal Arithmetic
Now that you are fully convinced that handling money amounts with native JavaScript number type is a bad idea (at least I hope you begin to have doubts about it), the 1Billion$ question is how should you proceed ? A solution could be to make use of some of the powerful fixed-precision arithmetic packages available in JavaScript. For example Decimal.js (which is used by the popular ORM Prisma to represent its Decimal datatype) or Big.js.
These packages provide you with special datatypes that allow you to perform calculations with getting rid of precision errors we explained above.
// Example using Decimal.js
const Decimal = require('decimal.js');
const a = new Decimal('0.1');
const b = new Decimal('0.2');
const result = a.plus(b);
console.log(result.toString()); // Output: '0.3'
This approach provides you with another advantage, it drastically extends the maximum value that can be represented, which can become pretty handy when you are dealing with cryptocurrencies for example.
Even if it is really robust, that it not the one I prefer to choose to implement in my web applications. I find it easier and clearer to apply Stripe strategy to only deal with integer values.
Learn from Masters : Stripe, a No-Floating Points Strategy
We, at Theodo Fintech, value pragmatism! We love to take inspiration from the most succeeding companies in the industry. Stripe, the well-known billions$ company specialized in payment services, made the choice to handle money amounts without floating numbers but with integers. To do that, they use the smallest unit of the currency to represent a monetary amount.
// 10 USD are represented by
{
"amount": 1000,
"currency": "USD"
}
Currency Minimal Units… Are Not Consistent!
I guess that many of you already know this: all currencies don't have the smallest unit of the same magnitude. Most of them are "two-decimal" currencies (EUR, USD, GBP) which means that their smallest unit is 1/100th of the currency. However, some are "three-decimal" currencies (KWD) or even "zero-decimal" currencies (JPY). (You can find more information about it by following the ISO4217 standard). To handle these disparities, you should integrate to your money data representation the multiplicative factor to convert an amount represented in the smallest unit into the corresponding currency.
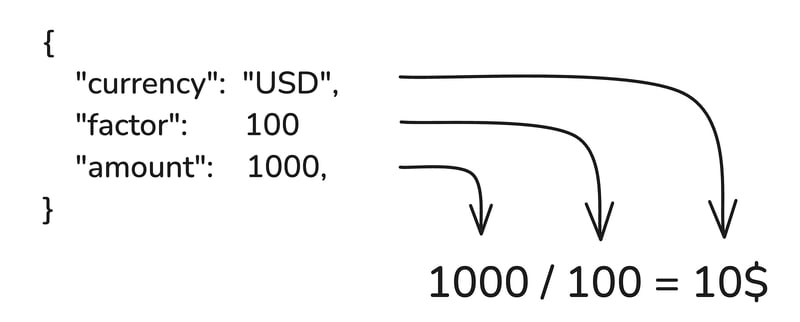
I Chose a Way to Represent Money Amount… OK, But Now, How Do I Round Them?
I guess you already figured it out, you can either work with native number , third party arbitrary-precision packages or integers, calculations can (and will) lead you to floating-point results that you will need to round to your monetary finite precision. As a quick example is never to much, let's say that you handle integer values and contracted a loan of 16k$ with a really precise interest rate of 8.5413% (ouch…). You then need to refund 16k$ plus an additional amount of
1600000 * 0.085413 // amount in cents //Output in cents: 136660.8
The crux is to properly handle the rounding process of money amounts after calculations. Most of the time, you end up having to choose between three different kinds of rounding:
- Classic rounding: Round to the closest value and if halfway between two values, round up
- Banker rounding: Round to the closest value and if halfway between two values, round down if the number is even, and round up if the number is odd (this gives you numerical stability when you have to perform lots of rounding)
- Custom rounding: based on particular legislation for the currency you use and the use case you are handling
When it comes to roundings, there is not really any "magic sauce": you need to arbitrate depending on your situation. I recommend you always check legislation when you deal with a new currency and a new rounding use case (conversion, money split, interest rates for credits, …). You better follow regulations right away to avoid further troubles. For example, when it comes to conversion rates, most currencies have determined rules about needed precision and rounding rules (you can have a look at the EUR conversion rate rules here).
Abschluss
Dieser Artikel erhebt keinen Anspruch auf Vollständigkeit aller vorhandenen Möglichkeiten zur Verarbeitung von Geldbeträgen in JavaScript und ist auch nicht dazu gedacht, Ihnen ein vollständiges/perfektes Gelddatenmodell zu bieten. Ich habe versucht, Ihnen genügend Hinweise und Richtlinien zu geben, um eine Darstellung umzusetzen, die sich als konsistent und belastbar erwiesen hat und die von großen Akteuren der Fintech-Branche gewählt wurde. Ich hoffe, dass Sie in Ihren zukünftigen Projekten Geldbeträge berechnen können, ohne einen Cent in Ihrer Tasche zu vergessen (ansonsten vergessen Sie nicht, einen Blick in Ihre alte Jacke zu werfen)!
Das obige ist der detaillierte Inhalt vonFinanzielle Präzision in JavaScript: Mit Geld umgehen, ohne einen Cent zu verlieren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse

