Heim >Web-Frontend >js-Tutorial >Drachenkurve 2

Drachenkurve 2

WBOYOriginal: 2024-08-08 16:30:22813Durchsuche

Ich möchte die Drachenkurve in fünf Sprachlösungen zeigen:

Pascal
Python
Schildkröte
Delphi
Java Script

Eine Drachenkurve ist jedes Mitglied einer Familie selbstähnlicher fraktaler Kurven, die durch rekursive Methoden wie Lindenmayer-Systeme angenähert werden können, wie ein Verfahren in Pascal zeigt:

procedure Dragon(n,a,t:Integer; d,x,y: Double; var b: TBitmap);
  var a1, a2: integer;
begin
 if n <= 1 then begin
   with b.Canvas do begin
     Pen.Color:= random(p);
     MoveTo(Trunc(x + 0.5), Trunc(y + 0.5));
     LineTo(Trunc(x + d *_cos[a]+0.5),Trunc(y+d *_sin[a]+0.5));
     exit;
   end;
 end;
 d:= d * s;
 a1:= (a - t) and 7;
 a2:= (a + t) and 7;
 dragon(n - 1, a1, 1, d, x, y, b);
 dragon(n - 1, a2, -1, d, x + d *_cos[a1], y + d *_sin[a1], b);
end;

Rekursiv ist ein rechts gekrümmter Drache ein rechter Drache, gefolgt von einem linken Drachen, im 90-Grad-Winkel. Und ein linker Drache ist ein linker, gefolgt von einem rechten. Das Gleiche erhalten Sie auch mit Python und Turtle in maXbox:

Const DRAGFUNC =
  'def dragon(level=4, size=200, direction=45):   '+LF+
  '  if level:                                     '+LF+
  '      right(direction)                          '+LF+
  '      dragon(level-1, size/1.41421356237, 45)   '+LF+
  '      left(direction * 2)                       '+LF+
  '      dragon(level-1, size/1.41421356237, -45)  '+LF+
  '      right(direction)                          '+LF+
  '  else:                                         '+LF+
  '      forward(size)                             ';

function PyCodeDragonTurtle(imgpath, aAPIKey: string): string;
begin
  with TPythonEngine.Create(Nil) do begin
  //pythonhome:= 'C:\Users\User\AppData\Local\Programs\Python\Python312\';
  try
    loadDLL;
    autofinalize:= false;
    ExecString('from turtle import right,left,forward,speed, exitonclick,hideturtle');
    ExecStr(DRAGFUNC); 
    ExecStr('speed(0)');  
    //ExecStr('hideturtle()'); 
    ExecStr('dragon(6)');
    ExecStr('exitonclick()');
    //result:= (EvalStr('r.json()')); *)
  except
    raiseError;        
  finally      
    Free;
  end; 
 end;
end;

Die Drachenkurve wird wahrscheinlich am häufigsten als die Form angesehen, die durch wiederholtes Falten eines Papierstreifens in zwei Hälften entsteht.

Dragon Curve 2
Drache als Pen.Color:= (p);

Das Skript erhalten Sie unter:
Mehrsprachiges Skript

https://sourceforge.net/projects/maxbox/files/Examples/13_General/1320_dragon_curve_51_py.txt/download

Dragon Curve 2
mit Tiefe = 9

Dragon Curve 2

Dragon Curve 2
Stiftbreite:= 2; Pen.Color := cllime;

Schildkrötengeräusch

Dragon Curve 2
Probieren Sie den Schildkrötenklang mit Winkel als Amplitude und Schritt als Ton aus:

procedure DrawDragon2(step, adir: integer; len:real);
begin
  //myturtle:= TJvTurtle.create(self);
  with myturtle do begin
    if (step >-1) and (len >1) then begin
      len:= len /sqrt(2);
      Turn(45*adir);
        DrawDragon2(step-1, +1, len);
      Turn(-90*adir);
        DrawDragon2(step-1, -1, len);
      Turn(45*adir);
    end else      //*)
      moveforward(len )
  end;  
end;

Dragon Curve 2

JavaScript eingebettet

Mit dem Microsoft Edge WebView2-Steuerelement können Sie Webtechnologien (HTML, CSS und JavaScript) in Ihre nativen Apps einbetten. Das WebView2-Steuerelement verwendet Microsoft Edge als Rendering-Engine, um den Webinhalt in nativen Apps anzuzeigen.

Dragon Curve 2

<!-- DragonCurve.html -->
<html>
<head>
<script type='text/javascript'>
function pDragon(cId) {
  // Plotting Dragon curves. 2/25/17 aev
  var n=document.getElementById('ord').value;
  var sc=document.getElementById('sci').value;
  var hsh=document.getElementById('hshi').value;
  var vsh=document.getElementById('vshi').value;
  var clr=document.getElementById('cli').value;
  var c=c1=c2=c2x=c2y=x=y=0, d=1, n=1<<n;
  var cvs=document.getElementById(cId);
  var ctx=cvs.getContext("2d");
  hsh=Number(hsh); vsh=Number(vsh);
  x=y=cvs.width/2;
  // Cleaning canvas, init plotting
  ctx.fillStyle="white"; ctx.fillRect(0,0,cvs.width,cvs.height);
  ctx.beginPath();
  for(i=0; i<=n;) {
    ctx.lineTo((x+hsh)*sc,(y+vsh)*sc);
    c1=c&1; c2=c&2;
    c2x=1*d; if(c2>0) {c2x=(-1)*d}; c2y=(-1)*c2x;
    if(c1>0) {y+=c2y} else {x+=c2x}
    i++; c+=i/(i&-i);
  }
  ctx.strokeStyle = clr;  ctx.stroke();
}
</script>
</head>
<body>
<p><b>Please input order, scale, x-shift, y-shift, color:</></p>
<input id=ord value=11 type="number" min="7" max="25" size="2">
<input id=sci value=7.0 type="number" min="0.001" max="10" size="5">
<input id=hshi value=-265 type="number" min="-50000" max="50000" size="6">
<input id=vshi value=-260 type="number" min="-50000" max="50000" size="6">
<input id=cli value="red" type="text" size="14">
<button onclick="pDragon('canvId')">Plot it!</button>
<h3>Dragon curve</h3>
<canvas id="canvId" width=640 height=640 style="border: 2px inset;"></canvas>
</body>
</html>

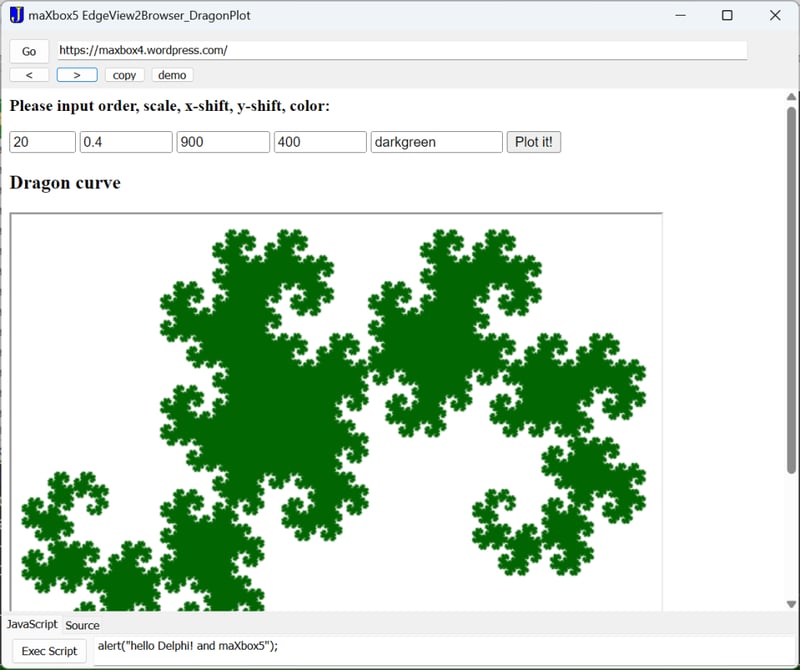
Dragon Curve 2
Ändern und erkunden Sie in EdgeView von maXbox5
Das Skript finden Sie unter:

das gesamte 5-Sprachen-Skript unter

Das obige ist der detaillierte Inhalt vonDrachenkurve 2. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Python Java JavaScript css html edge try display https microsoft

Stellungnahme：

Der Inhalt dieses Artikels wird freiwillig von Internetnutzern beigesteuert und das Urheberrecht liegt beim ursprünglichen Autor. Diese Website übernimmt keine entsprechende rechtliche Verantwortung. Wenn Sie Inhalte finden, bei denen der Verdacht eines Plagiats oder einer Rechtsverletzung besteht, wenden Sie sich bitte an admin@php.cn

Vorheriger Artikel：Der ultimative Leitfaden zu API-Architekturen zur Auswahl des richtigen Ansatzes für Ihr ProjektNächster Artikel：Der ultimative Leitfaden zu API-Architekturen zur Auswahl des richtigen Ansatzes für Ihr Projekt

In Verbindung stehende Artikel

Mehr sehen