Heim >Web-Frontend >js-Tutorial >Eine Reise durch Algorithmen mit Javascript – Bubble Sort
Eine Reise durch Algorithmen mit Javascript – Bubble Sort
- PHPzOriginal
- 2024-07-29 06:30:53523Durchsuche
Was ist Blasensortierung?
Bubble Sort ist einer der einfachsten Sortieralgorithmen in der Informatik. Benannt nach der Art und Weise, wie kleinere Elemente bei jeder Iteration an den Anfang der Liste „sprudeln“, ist es ein hervorragendes Werkzeug, um die Grundlagen von Sortieralgorithmen zu vermitteln. Obwohl es für große Datenmengen nicht besonders effizient ist, ist es aufgrund seiner Einfachheit ein guter Ausgangspunkt für das Verständnis der Funktionsweise von Sortieralgorithmen.
So funktioniert die Blasensortierung
Bubble Sort funktioniert, indem es wiederholt durch die Liste geht, benachbarte Elemente vergleicht und sie vertauscht, wenn sie in der falschen Reihenfolge sind. Dieser Vorgang wird wiederholt, bis keine weiteren Swaps mehr erforderlich sind, was anzeigt, dass die Liste sortiert ist.
Hier ist eine Schritt-für-Schritt-Anleitung:
- Beginnen Sie mit dem ersten Element im Array.
- Vergleichen Sie es mit dem nächsten Element.
- Wenn das erste Element größer als das zweite ist, tauschen Sie sie aus.
- Gehen Sie zum nächsten Element und wiederholen Sie die Schritte 2-3, bis Sie das Ende des Arrays erreicht haben.
- Wenn ein Austausch vorgenommen wurde, wiederholen Sie den Vorgang von Anfang an.
- Wenn in einem vollständigen Durchgang keine Swaps durchgeführt wurden, wird das Array sortiert.
Lassen Sie uns diesen Prozess visualisieren:
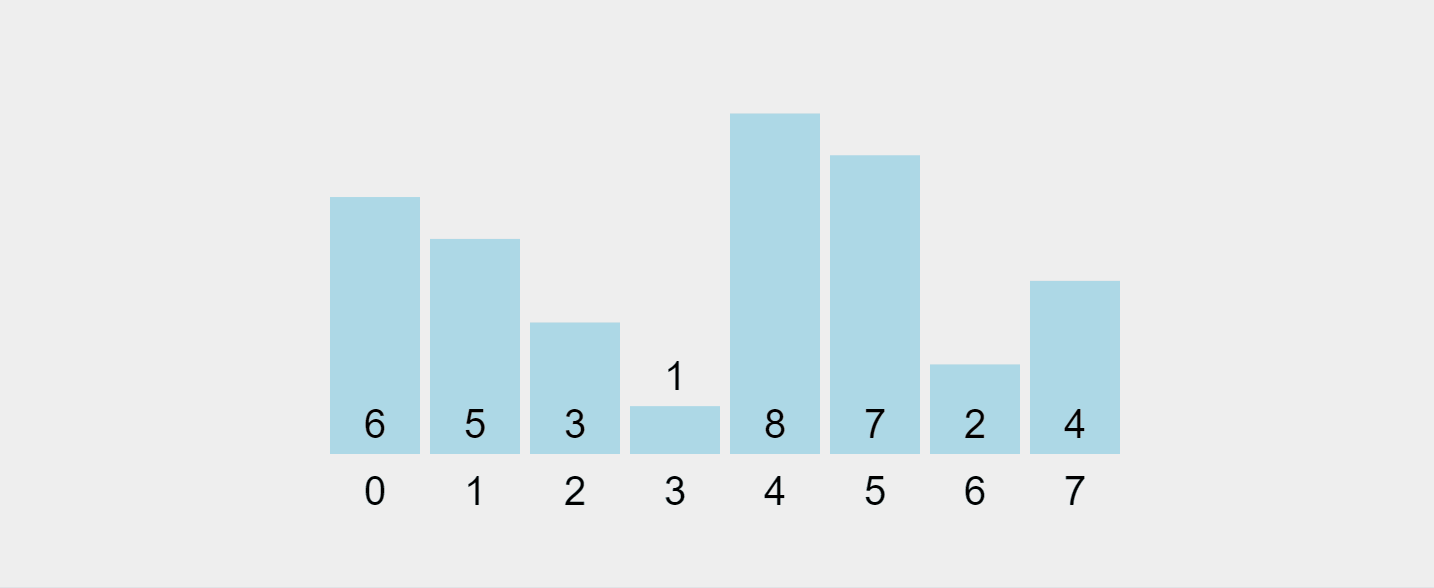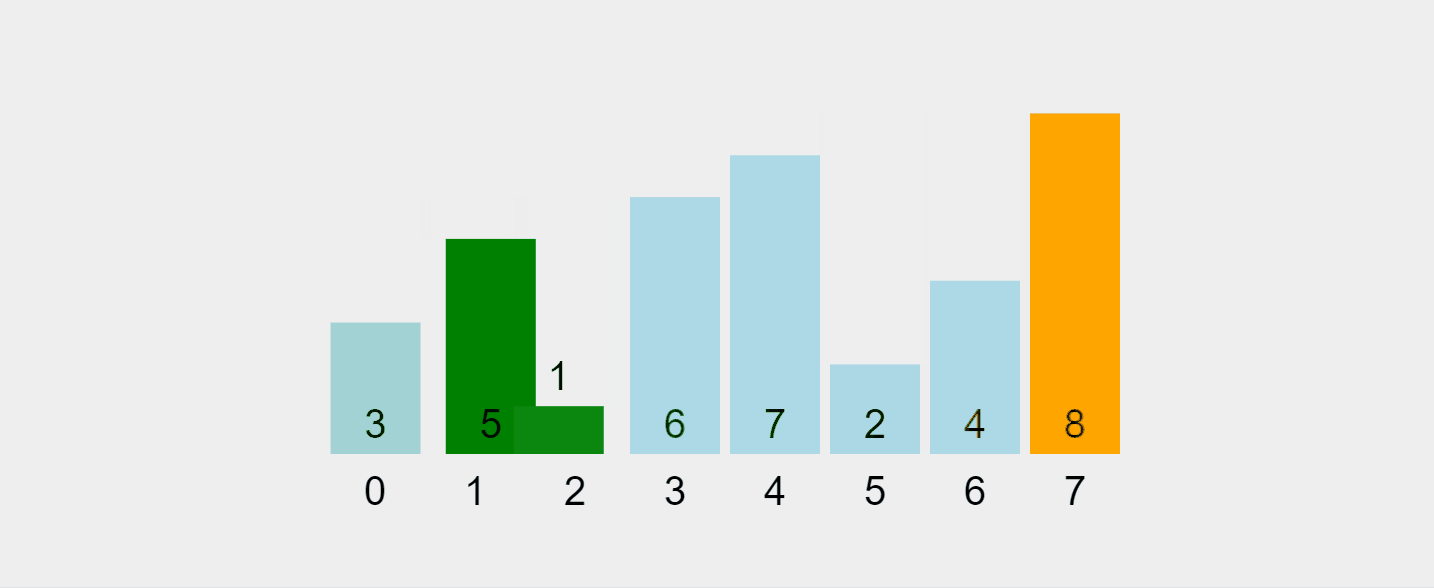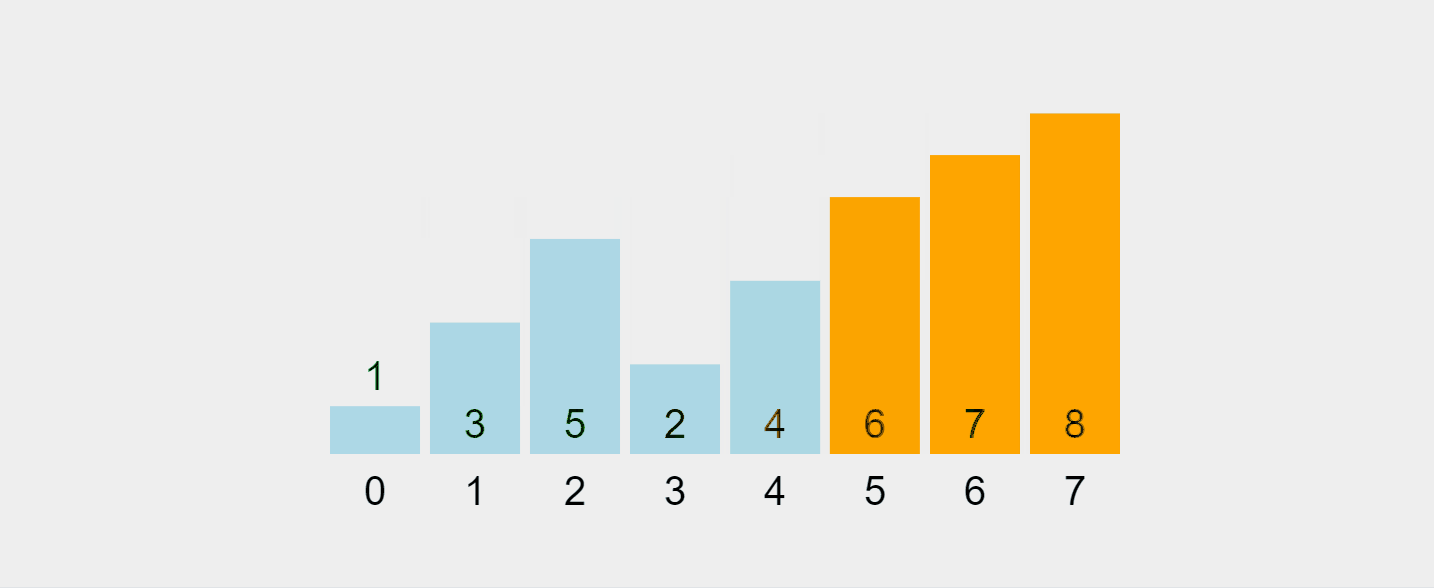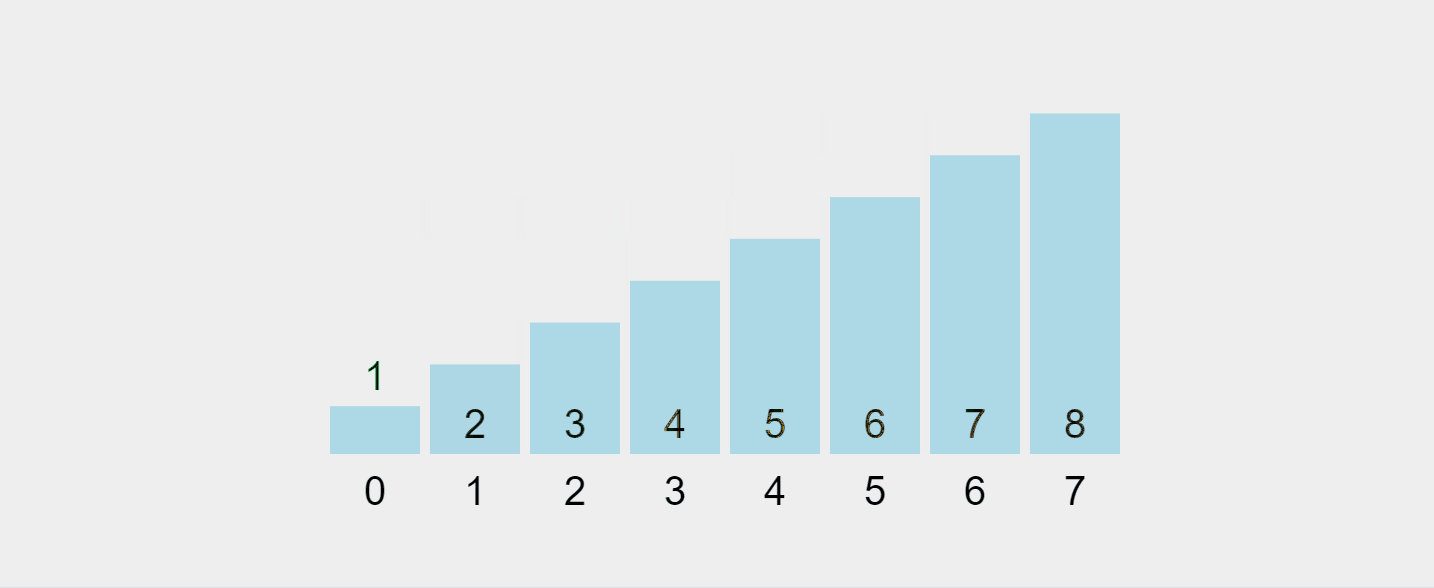
Aufgezeichnetes GIF von https://visualgo.net/en/sorting
Implementieren der Blasensortierung in JavaScript
Untersuchen wir drei Implementierungen von Bubble Sort in JavaScript, jeweils mit zunehmendem Optimierungsgrad.
Grundlegende Implementierung (v1)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Inner loop: compare adjacent elements
for (let j = 0; j < list.length - 1; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
}
}
}
// Return the sorted list
return list;
}
Diese grundlegende Implementierung verwendet verschachtelte Schleifen, um benachbarte Elemente zu vergleichen und auszutauschen. Die äußere Schleife stellt sicher, dass wir genügend Durchläufe durch das Array machen, während die innere Schleife die Vergleiche und Swaps durchführt.
Optimierte Implementierung (v2)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Flag to check if any swaps occurred in this pass
let swapped = false;
// Inner loop: compare adjacent elements
for (let j = 0; j < list.length - 1; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
// Set the swapped flag to true
swapped = true;
}
}
// If no swaps occurred in this pass, the list is sorted
if (!swapped) {
break; // Exit the outer loop early
}
}
// Return the sorted list
return list;
}
Diese Version führt ein Swap-Flag ein, um zu überprüfen, ob in einem Durchgang Swaps vorgenommen wurden. Wenn keine Vertauschungen stattfinden, ist die Liste bereits sortiert und wir können die Schleife frühzeitig verlassen.
Am besten optimierte Implementierung (v3)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Flag to check if any swaps occurred in this pass
let swapped = false;
// Inner loop: compare adjacent elements
// Note: We reduce the upper bound by i in each pass
for (let j = 0; j < list.length - 1 - i; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
// Set the swapped flag to true
swapped = true;
}
}
// If no swaps occurred in this pass, the list is sorted
if (!swapped) {
break; // Exit the outer loop early
}
}
// Return the sorted list
return list;
}
Diese letzte Optimierung reduziert den Bereich der inneren Schleife in jedem Durchgang um i. Dies liegt daran, dass nach jedem Durchgang das größte unsortierte Element an seine korrekte Position am Ende des Arrays „aufsteigt“.
Zeit- und Raumkomplexitätsanalyse
Die Leistungsmerkmale von Bubble Sort sind wie folgt:
-
Zeitkomplexität:
- Bester Fall: O(n) – wenn das Array bereits sortiert ist
- Durchschnittlicher Fall: O(n^2)
- Schlimmster Fall: O(n^2) – wenn das Array in umgekehrter Reihenfolge ist
Raumkomplexität: O(1) – Bubble Sort ist ein In-Place-Sortieralgorithmus, der nur eine konstante Menge an zusätzlichem Speicher benötigt.
Im Vergleich zu fortgeschritteneren Algorithmen wie Quick Sort (durchschnittliches O(n log n)) oder Merge Sort (O(n log n)) ist Bubble Sort aufgrund seiner quadratischen Zeitkomplexität für große Datensätze ineffizient.
Vor- und Nachteile der Blasensortierung
Vorteile:
- Einfach zu verstehen und umzusetzen
- In-Place-Sortierung (O(1)-Raum)
- Stabiler Sortieralgorithmus
- Kann bereits sortierte Listen erkennen
Nachteile:
- Ineffizient für große Datensätze (O(n^2))
- Schlechte Leistung bei nahezu sortierten Daten
- Übermäßige Austauschvorgänge
Wann sollte die Blasensortierung verwendet werden?
- Bildungszwecke: Aufgrund seiner Einfachheit eignet es sich hervorragend für die Vermittlung grundlegender Algorithmuskonzepte.
- Kleine Datensätze: Bei sehr kleinen Arrays kann der Leistungsunterschied im Vergleich zu komplexen Algorithmen vernachlässigbar sein.
- Fast sortierte Daten: Mit der optimierten Version kann es bei fast sortierten Listen einigermaßen effizient sein.
- Umgebungen mit begrenztem Speicher: Seine In-Place-Natur kann in Szenarien mit extrem begrenztem Speicher von Vorteil sein.
Cocktailsorte: Eine verbesserte Variante
Cocktail Sort, auch bekannt als Cocktail Shake Sort oder Bidirektionale Bubble Sort, ist eine verbesserte Version von Bubble Sort. Es durchläuft die Liste in beide Richtungen und trägt so dazu bei, Elemente effizienter an ihre richtigen Positionen zu verschieben.
How Cocktail Sort Works
- Start with the first element and move towards the end, swapping adjacent elements if they're in the wrong order.
- When you reach the end, start from the second-to-last element and move towards the beginning, again swapping elements as needed.
- Repeat this process, narrowing the range of elements to check with each pass, until no swaps are needed.
Cocktail Sort is particularly useful in cases where the array has elements that are initially large at the beginning and small at the end, as it can reduce the total number of passes needed compared to traditional Bubble Sort.
Here's a visualization of Cocktail Sort:
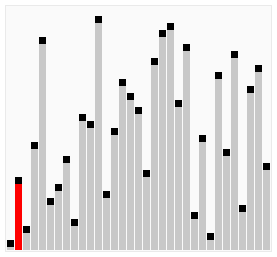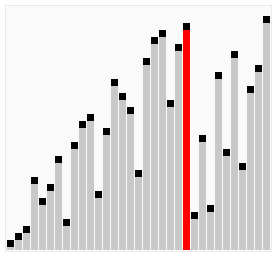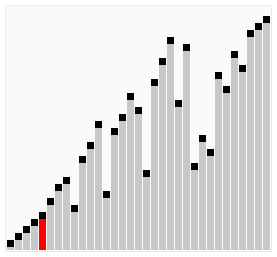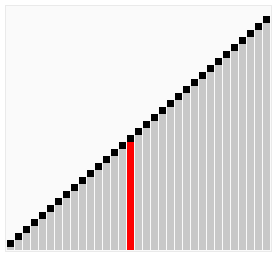
Visual from Wikipedia: https://en.wikipedia.org/wiki/Cocktail_shaker_sort
Cocktail Sort implementation in Javascript
function cocktailSort(list) {
let swapped;
// The do...while loop ensures the sorting continues until no swaps are needed
do {
// Reset the swapped flag at the beginning of each complete iteration
swapped = false;
// First pass: left to right (like standard bubble sort)
for (let i = 0; i < list.length - 1; i++) {
// If the current element is greater than the next, swap them
if (list[i] > list[i + 1]) {
[list[i], list[i + 1]] = [list[i + 1], list[i]];
// Mark that a swap occurred
swapped = true;
}
}
// If no swaps occurred in the first pass, the array is sorted
if (!swapped) {
break; // Exit the do...while loop early
}
// Reset the swapped flag for the second pass
swapped = false;
// Second pass: right to left (this is what makes it "cocktail" sort)
for (let i = list.length - 2; i >= 0; i--) {
// If the current element is greater than the next, swap them
if (list[i] > list[i + 1]) {
[list[i], list[i + 1]] = [list[i + 1], list[i]];
// Mark that a swap occurred
swapped = true;
}
}
// The loop will continue if any swaps occurred in either pass
} while (swapped);
// Return the sorted list
return list;
}
This implementation alternates between forward and backward passes through the list, potentially reducing the number of iterations needed to sort the array.
Practical Applications and Use Cases
While Bubble Sort isn't typically used in production environments for large-scale applications, it can still find use in certain scenarios:
- Educational tools: It's often used to introduce sorting algorithms and algorithm analysis in computer science education.
- Embedded systems: In systems with very limited memory, its in-place sorting can be advantageous.
- Small datasets: For sorting small lists (e.g., less than 50 elements), its simplicity might outweigh the performance benefits of more complex algorithms.
- Nearly sorted data: If data is known to be almost sorted, an optimized Bubble Sort can be reasonably efficient.
- Sorting stability requirement: When a stable sort is needed and simplicity is preferred over efficiency, Bubble Sort can be a straightforward choice.
Conclusion
Bubble Sort, despite its inefficiencies with large datasets, offers valuable insights into the world of sorting algorithms and algorithm analysis. Its straightforward approach makes it an excellent teaching tool for beginners in computer science.
Key takeaways are:
- It's simple to understand and implement.
- It has a time complexity of O(n^2), making it inefficient for large datasets.
- It's an in-place and stable sorting algorithm.
- Optimizations can improve its performance, especially for nearly sorted data.
- It's primarily used for educational purposes and in scenarios with very small datasets or limited memory.
While you're unlikely to use Bubble Sort in production code for large-scale applications, the principles behind it are fundamental to many algorithms. The process of optimizing Bubble Sort teaches valuable lessons about algorithm improvement, serving as a stepping stone to more advanced computational problem-solving.
When it comes to algorithms, there's rarely a one-size-fits-all solution. The best algorithm for a given task depends on the specific requirements, constraints, and characteristics of your data. Bubble Sort, with all its limitations, still has its place in this diverse algorithmic ecosystem.
Das obige ist der detaillierte Inhalt vonEine Reise durch Algorithmen mit Javascript – Bubble Sort. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse

