Heim >Java >javaLernprogramm >Testen der AVLTree-Klasse
Testen der AVLTree-Klasse
- 王林Original
- 2024-07-25 09:09:31782Durchsuche
Dieser Abschnitt enthält ein Beispiel für die Verwendung der Klasse AVLTree. Der folgende Code gibt ein Testprogramm an. Das Programm erstellt einen AVLTree, der mit einem Array der Ganzzahlen 25, 20 und 5 initialisiert ist (Zeilen 7) und fügt Elemente ein Zeilen 11–20 und löscht Elemente in den Zeilen 24–30. Da AVLTree eine Unterklasse von BST ist und die Elemente in einem BST iterierbar sind, verwendet das Programm eine foreach-Schleife, um alle Elemente in den Zeilen 35–37 zu durchlaufen .
package demo;
public class TestAVLTree {
public static void main(String[] args) {
// Create an AVL tree
AVLTree<Integer> tree = new AVLTree<>(new Integer[]{25, 20, 5});
System.out.print("After inserting 25, 20, 5:");
printTree(tree);
tree.insert(34);
tree.insert(50);
System.out.print("\nAfter inserting 34, 50:");
printTree(tree);
tree.insert(30);
System.out.print("\nAfter inserting 30");
printTree(tree);
tree.insert(10);
System.out.print("\nAfter inserting 10");
printTree(tree);
tree.delete(34);
tree.delete(30);
tree.delete(50);
System.out.print("\nAfter removing 34, 30, 50:");
printTree(tree);
tree.delete(5);
System.out.print("\nAfter removing 5:");
printTree(tree);
System.out.print("\nTraverse the elements in the tree: ");
for (int e: tree) {
System.out.print(e + " ");
}
}
public static void printTree(BST tree) {
// Traverse tree
System.out.print("\nInorder (sorted): ");
tree.inorder();
System.out.print("\nPostorder: ");
tree.postorder();
System.out.print("\nPreorder: ");
tree.preorder();
System.out.print("\nThe number of nodes is " + tree.getSize());
System.out.println();
}
}
Nach dem Einfügen von 25, 20, 5:
In der Reihenfolge (sortiert): 5 20 25
Nachbestellung: 5 25 20
Vorbestellung: 20 5 25
Die Anzahl der Knoten beträgt 3
Nach dem Einfügen von 34, 50:
In der Reihenfolge (sortiert): 5 20 25 34 50
Nachbestellung: 5 25 50 34 20
Vorbestellung: 20 5 34 25 50
Die Anzahl der Knoten beträgt 5
Nach dem Einfügen von 30
In der Reihenfolge (sortiert): 5 20 25 30 34 50
Nachbestellung: 5 20 30 50 34 25
Vorbestellung: 25 20 5 34 30 50
Die Anzahl der Knoten beträgt 6
Nach dem Einfügen von 10
In der Reihenfolge (sortiert): 5 10 20 25 30 34 50
Nachbestellung: 5 20 10 30 50 34 25
Vorbestellung: 25 10 5 20 34 30 50
Die Anzahl der Knoten beträgt 7
Nach dem Entfernen von 34, 30, 50:
In der Reihenfolge (sortiert): 5 10 20 25
Nachbestellung: 5 20 25 10
Vorbestellung: 10 5 25 20
Die Anzahl der Knoten beträgt 4
Nach dem Entfernen von 5:
In der Reihenfolge (sortiert): 10 20 25
Nachbestellung: 10 25 20
Vorbestellung: 20 10 25
Die Anzahl der Knoten beträgt 3
Durchlaufen Sie die Elemente im Baum: 10 20 25
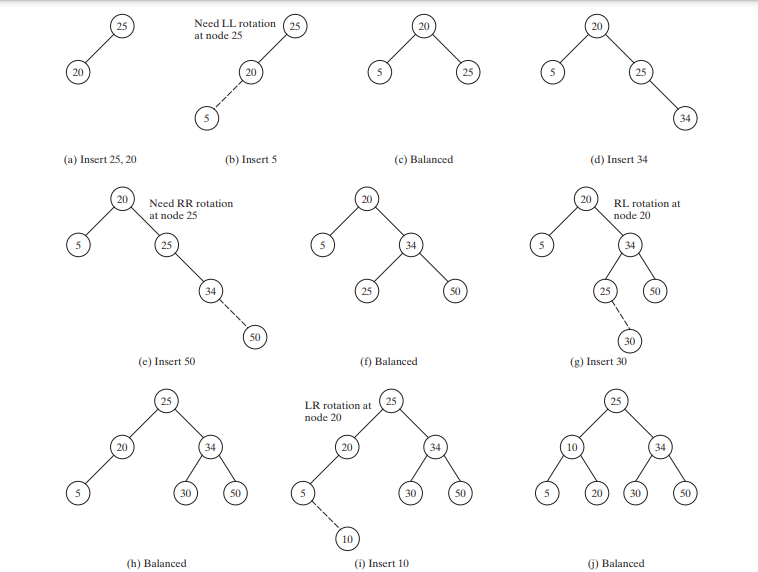
Die Abbildung unten zeigt, wie sich der Baum entwickelt, wenn Elemente zum Baum hinzugefügt werden. Nachdem 25 und 20 hinzugefügt wurden, sieht der Baum wie in Abbildung unten (a) dargestellt aus. 5 wird als linkes untergeordnetes Element von 20 eingefügt, wie in Abbildung unten (b) gezeigt. Der Baum ist nicht im Gleichgewicht. Am Knoten 25 ist es linkslastig. Führen Sie eine LL-Rotation durch, um einen AVL-Baum zu erhalten, wie in Abbildung unten (c) gezeigt.
Nach dem Einfügen von 34 ist der Baum in Abbildung unten (d) dargestellt. Nach dem Einfügen von 50 sieht der Baum wie in Abbildung unten (e) dargestellt aus. Der Baum ist nicht im Gleichgewicht. Am Knoten 25 ist es rechtslastig. Führen Sie eine RR-Rotation durch, um einen AVL-Baum zu erhalten, wie in Abbildung unten (f) gezeigt.
Nach dem Einfügen von 30 sieht der Baum wie in der Abbildung unten (g) aus. Der Baum ist nicht im Gleichgewicht. Führen Sie eine RL-Rotation durch, um einen AVL-Baum zu erhalten, wie in Abbildung unten (h) gezeigt.
Nach dem Einfügen von 10 sieht der Baum wie in Abbildung unten (i) aus. Der Baum ist nicht im Gleichgewicht. Führen Sie eine LR-Rotation durch, um einen AVL-Baum zu erhalten, wie in Abbildung unten (j) gezeigt.
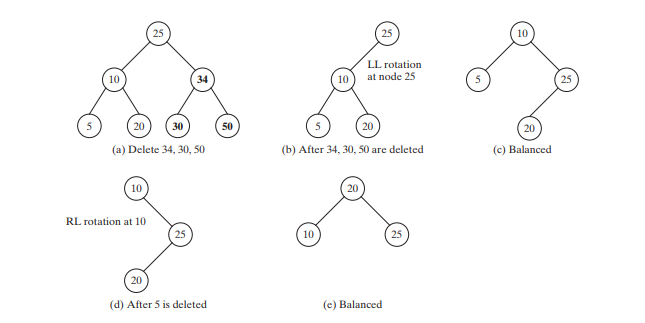
Die Abbildung unten zeigt, wie sich der Baum entwickelt, wenn Elemente gelöscht werden. Nach dem Löschen von 34, 30 und 50 sieht der Baum wie in Abbildung unten (b) dargestellt aus. Der Baum ist nicht im Gleichgewicht. Führen Sie eine LL-Rotation durch, um einen AVL-Baum zu erhalten, wie in Abbildung unten (c) gezeigt.
Nach dem Löschen von 5 sieht der Baum wie in Abbildung unten (d) dargestellt aus. Der Baum ist nicht im Gleichgewicht. Führen Sie eine RL-Rotation durch, um einen AVL-Baum zu erhalten, wie in Abbildung unten (e) gezeigt
Das obige ist der detaillierte Inhalt vonTesten der AVLTree-Klasse. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

