Logistische Regression, Klassifizierung: Überwachtes maschinelles Lernen

Was ist Klassifizierung?

Definition und Zweck

Klassifizierung ist eine überwachte Lerntechnik, die im maschinellen Lernen und in der Datenwissenschaft verwendet wird, um Daten in vordefinierte Klassen oder Bezeichnungen zu kategorisieren. Dabei wird ein Modell trainiert, um Eingabedatenpunkte basierend auf ihren Merkmalen einer von mehreren diskreten Kategorien zuzuordnen. Der Hauptzweck der Klassifizierung besteht darin, die Klasse oder Kategorie neuer, unsichtbarer Datenpunkte genau vorherzusagen.

Hauptziele:

• Vorhersage: Zuweisen neuer Datenpunkte zu einer der vordefinierten Klassen.
• Schätzung: Bestimmung der Wahrscheinlichkeit, dass ein Datenpunkt zu einer bestimmten Klasse gehört.
• Beziehungen verstehen: Identifizieren, welche Merkmale für die Vorhersage der Klasse der Datenpunkte von Bedeutung sind.

Arten der Klassifizierung

1. Binäre Klassifizierung

• Beschreibung: Kategorisiert Daten in eine von zwei Klassen.
  • Beispiele: Spam-Erkennung (Spam oder nicht Spam), Krankheitsdiagnose (Krankheit oder keine Krankheit).
  • Zweck: Unterscheidet zwischen zwei verschiedenen Klassen.

2. Mehrklassenklassifizierung

• Beschreibung: Kategorisiert Daten in eine von drei oder mehr Klassen.
  • Beispiele: Handschriftliche Ziffernerkennung (Ziffern 0–9), Klassifizierung von Blumenarten (mehrere Arten).
  • Zweck: Behandelt Probleme, bei denen mehr als zwei Klassen vorherzusagen sind.

Was sind lineare Klassifikatoren?

Lineare Klassifikatoren sind eine Kategorie von Klassifizierungsalgorithmen, die eine lineare Entscheidungsgrenze verwenden, um verschiedene Klassen im Merkmalsraum zu trennen. Sie treffen Vorhersagen, indem sie die Eingabemerkmale durch eine lineare Gleichung kombinieren, die typischerweise die Beziehung zwischen den Merkmalen und den Zielklassenbezeichnungen darstellt. Der Hauptzweck linearer Klassifikatoren besteht darin, Datenpunkte effizient zu klassifizieren, indem sie eine Hyperebene finden, die den Merkmalsraum in verschiedene Klassen unterteilt.

Logistische Regression

Definition und Zweck

Logistische Regression ist eine statistische Methode, die für binäre Klassifizierungsaufgaben im maschinellen Lernen und in der Datenwissenschaft verwendet wird. Es ist Teil von linearen Klassifikatoren und unterscheidet sich von der linearen Regression durch die Vorhersage der Eintrittswahrscheinlichkeit eines Ereignisses durch Anpassen der Daten an eine logistische Kurve.

Hauptziele:

• Binäre Klassifizierung: Vorhersage eines binären Ergebnisses (z. B. ja/nein, wahr/falsch).
• Wahrscheinlichkeitsschätzung: Schätzung der Wahrscheinlichkeit des Eintretens eines Ereignisses basierend auf Eingabevariablen.
• Entscheidungsgrenze: Bestimmen eines Schwellenwerts zur Klassifizierung von Daten in verschiedene Klassen.

Logistisches Regressionsmodell

1. Logistische Funktion (Sigmoidfunktion)

• Beschreibung: Die Logistikfunktion wandelt jede reelle Eingabe in einen Wert zwischen 0 und 1 um, wodurch sie für die Modellierung von Wahrscheinlichkeiten geeignet ist.
  • Gleichung: σ(z) = 1 / (1 + e^(-z))
  • Zweck: Ordnet die Eingabewerte Wahrscheinlichkeiten zu.

2. Logistische Regressionsgleichung

• Beschreibung: Das logistische Regressionsmodell wendet die logistische Funktion auf eine lineare Kombination von Eingabevariablen an.
  • Gleichung: P(y=1|x) = σ(w0 + w1x1 + w2x2 + ... + wnxn)
  • Zweck: Sagt die Wahrscheinlichkeit P(y=1|x) des binären Ergebnisses y=1 bei gegebenen Eingabevariablen x voraus.

Maximum-Likelihood-Schätzung (MLE)

MLE wird verwendet, um die Parameter (Koeffizienten) des logistischen Regressionsmodells zu schätzen, indem die Wahrscheinlichkeit der Beobachtung der vom Modell gegebenen Daten maximiert wird.

Gleichung: Die Maximierung der Log-Likelihood-Funktion beinhaltet das Finden der Parameter, die die Wahrscheinlichkeit der Beobachtung der Daten maximieren.

Kostenfunktion und Verlustminimierung in der logistischen Regression

Kostenfunktion

Die Kostenfunktion in der logistischen Regression misst den Unterschied zwischen vorhergesagten Wahrscheinlichkeiten und tatsächlichen Klassenbezeichnungen. Ziel ist es, diese Funktion zu minimieren, um die Vorhersagegenauigkeit des Modells zu verbessern.

Protokollverlust (binäre Kreuzentropie):
Die Protokollverlustfunktion wird häufig in der logistischen Regression für binäre Klassifizierungsaufgaben verwendet.

Log-Verlust = -(1/n) * Σ [y * log(ŷ) + (1 - y) * log(1 - ŷ)]

wo:

• y ist die tatsächliche Klassenbezeichnung (0 oder 1),
• ŷ ist die vorhergesagte Wahrscheinlichkeit der Klassenbezeichnung,
• n ist die Anzahl der Datenpunkte.

Der Protokollverlust bestraft Vorhersagen, die weit von der tatsächlichen Klassenbezeichnung entfernt sind, und ermutigt das Modell, genaue Wahrscheinlichkeiten zu erzeugen.

Verlustminimierung (Optimierung)

Verlustminimierung bei der logistischen Regression beinhaltet das Finden der Werte der Modellparameter, die den Kostenfunktionswert minimieren. Dieser Prozess wird auch als Optimierung bezeichnet. Die gebräuchlichste Methode zur Verlustminimierung bei der logistischen Regression ist der Gradient Descent-Algorithmus.

Gefälleabstieg

Gradient Descent ist ein iterativer Optimierungsalgorithmus, der zur Minimierung der Kostenfunktion in der logistischen Regression verwendet wird. Es passt die Modellparameter in Richtung des steilsten Abfalls der Kostenfunktion an.

Schritte des Gradientenabstiegs:

1. Parameter initialisieren: Beginnen Sie mit Anfangswerten für die Modellparameter (z. B. Koeffizienten w0, w1, ..., wn).

2. Steigung berechnen: Berechnen Sie den Gradienten der Kostenfunktion in Bezug auf jeden Parameter. Der Gradient ist die partielle Ableitung der Kostenfunktion.

3. Parameter aktualisieren: Passen Sie die Parameter in die entgegengesetzte Richtung des Farbverlaufs an. Die Anpassung wird durch die Lernrate (α) gesteuert, die die Größe der Schritte in Richtung des Minimums bestimmt.

4. Wiederholen: Iterieren Sie den Prozess, bis die Kostenfunktion einem Mindestwert konvergiert (oder eine vordefinierte Anzahl von Iterationen erreicht ist).

Parameteraktualisierungsregel:
Für jeden Parameter wj:
wj = wj - α * (∂/∂wj) Protokollverlust

wo:

• α ist die Lernrate,
• (∂/∂wj) Log-Verlust ist die partielle Ableitung des Log-Verlusts nach wj.

Die partielle Ableitung des logarithmischen Verlusts nach wj kann wie folgt berechnet werden:
(∂/∂wj) Log-Verlust = -(1/n) * Σ [ (yi - ŷi) * xij / (ŷi * (1 - ŷi)) ]

wo:

• xij ist der Wert der j-ten unabhängigen Variablen für den i-ten Datenpunkt,
• ŷi ist die vorhergesagte Wahrscheinlichkeit der Klassenbezeichnung für den i-ten Datenpunkt.

Beispiel für eine logistische Regression (binäre Klassifizierung).

Logistische Regression ist eine Technik, die für binäre Klassifizierungsaufgaben verwendet wird und die Wahrscheinlichkeit modelliert, dass eine bestimmte Eingabe zu einer bestimmten Klasse gehört. Dieses Beispiel zeigt, wie man eine logistische Regression mithilfe synthetischer Daten implementiert, die Leistung des Modells bewertet und die Entscheidungsgrenze visualisiert.

Beispiel für einen Python-Code

1. Bibliotheken importieren

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

Dieser Block importiert die notwendigen Bibliotheken für Datenmanipulation, Darstellung und maschinelles Lernen.

2. Beispieldaten generieren

np.random.seed(42)  # For reproducibility
X = np.random.randn(1000, 2)
y = (X[:, 0] + X[:, 1] > 0).astype(int)

Dieser Block generiert Beispieldaten mit zwei Merkmalen, wobei die Zielvariable y basierend darauf definiert wird, ob die Summe der Merkmale größer als Null ist, wodurch ein binäres Klassifizierungsszenario simuliert wird.

3. Teilen Sie den Datensatz auf

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Dieser Block teilt den Datensatz zur Modellbewertung in Trainings- und Testsätze auf.

4. Erstellen und trainieren Sie das logistische Regressionsmodell

model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)

Dieser Block initialisiert das logistische Regressionsmodell und trainiert es mithilfe des Trainingsdatensatzes.

5. Machen Sie Vorhersagen

y_pred = model.predict(X_test)

Dieser Block verwendet das trainierte Modell, um Vorhersagen zum Testsatz zu treffen.

6. Bewerten Sie das Modell

accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)

print(f"Accuracy: {accuracy:.4f}")
print("\nConfusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)

Ausgabe:

Accuracy: 0.9950

Confusion Matrix:
[[ 92   0]
 [  1 107]]

Classification Report:
              precision    recall  f1-score   support

           0       0.99      1.00      0.99        92
           1       1.00      0.99      1.00       108

    accuracy                           0.99       200
   macro avg       0.99      1.00      0.99       200
weighted avg       1.00      0.99      1.00       200

Dieser Block berechnet und druckt die Genauigkeit, die Verwirrungsmatrix und den Klassifizierungsbericht und bietet Einblicke in die Leistung des Modells.

7. Visualisieren Sie die Entscheidungsgrenze

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                     np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Logistic Regression Decision Boundary")
plt.show()

Dieser Block visualisiert die vom logistischen Regressionsmodell erstellte Entscheidungsgrenze und veranschaulicht, wie das Modell die beiden Klassen im Merkmalsraum trennt.

Ausgabe:

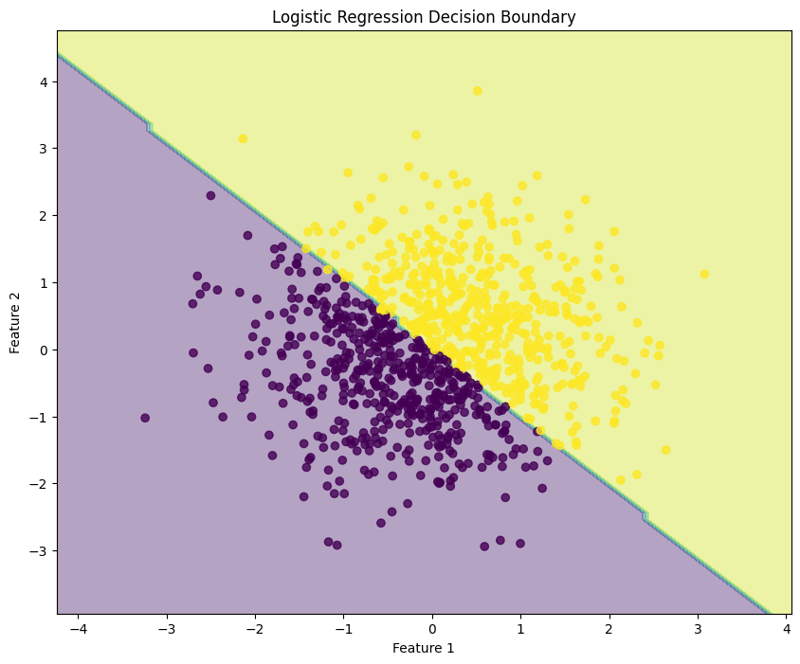
Dieser strukturierte Ansatz zeigt, wie die logistische Regression implementiert und ausgewertet wird, und vermittelt ein klares Verständnis ihrer Fähigkeiten für binäre Klassifizierungsaufgaben. Die Visualisierung der Entscheidungsgrenze hilft bei der Interpretation der Modellvorhersagen.

Logistic Regression (Multiclass Classification) Example

Logistic regression can also be applied to multiclass classification tasks. This example demonstrates how to implement logistic regression using synthetic data, evaluate the model's performance, and visualize the decision boundary for three classes.

Python Code Example

1. Import Libraries

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

This block imports the necessary libraries for data manipulation, plotting, and machine learning.

2. Generate Sample Data with 3 Classes

np.random.seed(42)  # For reproducibility
n_samples = 999  # Total number of samples
n_samples_per_class = 333  # Ensure this is exactly n_samples // 3

# Class 0: Top-left corner
X0 = np.random.randn(n_samples_per_class, 2) * 0.5 + [-2, 2]

# Class 1: Top-right corner
X1 = np.random.randn(n_samples_per_class, 2) * 0.5 + [2, 2]

# Class 2: Bottom center
X2 = np.random.randn(n_samples_per_class, 2) * 0.5 + [0, -2]

# Combine the data
X = np.vstack([X0, X1, X2])
y = np.hstack([np.zeros(n_samples_per_class), 
               np.ones(n_samples_per_class), 
               np.full(n_samples_per_class, 2)])

# Shuffle the dataset
shuffle_idx = np.random.permutation(n_samples)
X, y = X[shuffle_idx], y[shuffle_idx]

This block generates synthetic data for three classes located in different regions of the feature space.

3. Split the Dataset

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

This block splits the dataset into training and testing sets for model evaluation.

4. Create and Train the Logistic Regression Model

model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)

This block initializes the logistic regression model and trains it using the training dataset.

5. Make Predictions

y_pred = model.predict(X_test)

This block uses the trained model to make predictions on the test set.

6. Evaluate the Model

accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)

print(f"Accuracy: {accuracy:.4f}")
print("\nConfusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)

Output:

Accuracy: 1.0000

Confusion Matrix:
[[54  0  0]
 [ 0 65  0]
 [ 0  0 81]]

Classification Report:
              precision    recall  f1-score   support

         0.0       1.00      1.00      1.00        54
         1.0       1.00      1.00      1.00        65
         2.0       1.00      1.00      1.00        81

    accuracy                           1.00       200
   macro avg       1.00      1.00      1.00       200
weighted avg       1.00      1.00      1.00       200

This block calculates and prints the accuracy, confusion matrix, and classification report, providing insights into the model's performance.

7. Visualize the Decision Boundary

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                     np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.4, cmap='RdYlBu')
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, cmap='RdYlBu', edgecolor='black')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Multiclass Logistic Regression Decision Boundary")
plt.colorbar(scatter)
plt.show()

This block visualizes the decision boundaries created by the logistic regression model, illustrating how the model separates the three classes in the feature space.

Output:

This structured approach demonstrates how to implement and evaluate logistic regression for multiclass classification tasks, providing a clear understanding of its capabilities and the effectiveness of visualizing decision boundaries.

Evaluating Logistic Regression Model

Evaluating a logistic regression model involves assessing its performance in predicting binary or multiclass outcomes. Below are key methods for evaluation:

1. Performance Metrics

• Accuracy: The proportion of correctly classified instances out of the total instances. It provides a general sense of the model's performance.
  • Formula: Accuracy = (TP + TN) / (TP + TN + FP + FN)

  from sklearn.metrics import accuracy_score

  accuracy = accuracy_score(y_test, y_pred)
  print(f'Accuracy: {accuracy:.4f}')

• Confusion Matrix: A table that summarizes the performance of the classification model by showing the true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN).

  from sklearn.metrics import confusion_matrix

  conf_matrix = confusion_matrix(y_test, y_pred)
  print("\nConfusion Matrix:")
  print(conf_matrix)

• Precision: Measures the accuracy of the positive predictions. It is the ratio of true positives to the sum of true and false positives.
  • Formula: Precision = TP / (TP + FP)

  from sklearn.metrics import precision_score

  precision = precision_score(y_test, y_pred, average='weighted')
  print(f'Precision: {precision:.4f}')

• Recall (Sensitivity): Measures the model's ability to identify all relevant instances (true positives). It is the ratio of true positives to the sum of true positives and false negatives.
  • Formula: Recall = TP / (TP + FN)

  from sklearn.metrics import recall_score

  recall = recall_score(y_test, y_pred, average='weighted')
  print(f'Recall: {recall:.4f}')

• F1 Score: The harmonic mean of precision and recall, providing a balance between the two metrics. It is useful when the class distribution is imbalanced.
  • Formula: F1 Score = 2 * (Precision * Recall) / (Precision + Recall)

  from sklearn.metrics import f1_score

  f1 = f1_score(y_test, y_pred, average='weighted')
  print(f'F1 Score: {f1:.4f}')

2. Cross-Validation

Cross-validation techniques provide a more reliable evaluation of model performance by assessing it across different subsets of the dataset.

• K-Fold Cross-Validation: The dataset is divided into k subsets, and the model is trained on k-1 subsets while validating on the remaining subset. This is repeated k times, and the average metric provides a robust evaluation.

  from sklearn.model_selection import KFold, cross_val_score

  kf = KFold(n_splits=5, shuffle=True, random_state=42)
  scores = cross_val_score(model, X, y, cv=kf, scoring='accuracy')
  print(f'Cross-Validation Accuracy: {np.mean(scores):.4f}')

• Stratified K-Fold Cross-Validation: Similar to K-Fold but ensures that each fold maintains the class distribution, which is particularly beneficial for imbalanced datasets.

  from sklearn.model_selection import StratifiedKFold

  skf = StratifiedKFold(n_splits=5)
  scores = cross_val_score(model, X, y, cv=skf, scoring='accuracy')
  print(f'Stratified K-Fold Cross-Validation Accuracy: {np.mean(scores):.4f}')

By utilizing these evaluation methods and cross-validation techniques, practitioners can gain insights into the effectiveness of their logistic regression model and its ability to generalize to unseen data.

Regularization in Logistic Regression

Regularization helps mitigate overfitting in logistic regression by adding a penalty term to the loss function, encouraging simpler models. The two primary forms of regularization in logistic regression are L1 regularization (Lasso) and L2 regularization (Ridge).

L2-Regularisierung (Ridge Logistic Regression)

Konzept: Die L2-Regularisierung fügt der Verlustfunktion eine Strafe hinzu, die dem Quadrat der Größe der Koeffizienten entspricht.

Verlustfunktion: Die modifizierte Verlustfunktion für die logistische Ridge-Regression wird ausgedrückt als:

Verlust = -Σ[yi * log(ŷi) + (1 - yi) * log(1 - ŷi)] + λ * Σ(wj^2)

Wo:

• yi ist die eigentliche Klassenbezeichnung.
• ŷi ist die vorhergesagte Wahrscheinlichkeit der positiven Klasse.
• wj sind die Modellkoeffizienten.
• λ ist der Regularisierungsparameter.

Effekte:

• Ridge-Regularisierung schrumpft die Koeffizienten in Richtung Null, eliminiert sie jedoch nicht. Alle Merkmale bleiben im Modell erhalten, was für Fälle mit vielen Prädiktoren oder Multikollinearität von Vorteil ist.

L1-Regularisierung (Lasso-Logistische Regression)

Konzept: Die L1-Regularisierung fügt der Verlustfunktion eine Strafe hinzu, die dem absoluten Wert der Größe der Koeffizienten entspricht.

Verlustfunktion: Die modifizierte Verlustfunktion für die Lasso-Logistik-Regression kann ausgedrückt werden als:

Verlust = -Σ[yi * log(ŷi) + (1 - yi) * log(1 - ŷi)] + λ * Σ|wj|

Wo:

• yi ist die eigentliche Klassenbezeichnung.
• ŷi ist die vorhergesagte Wahrscheinlichkeit der positiven Klasse.
• wj sind die Modellkoeffizienten.
• λ ist der Regularisierungsparameter.

Effekte:

• Lasso-Regularisierung kann einige Koeffizienten auf genau Null setzen und so effektiv eine Variablenauswahl durchführen. Dies ist bei hochdimensionalen Datensätzen von Vorteil, bei denen die Interpretierbarkeit unerlässlich ist.

Durch die Anwendung von Regularisierungstechniken in der logistischen Regression können Praktiker die Modellverallgemeinerung verbessern und den Kompromiss zwischen Bias und Varianz effektiv verwalten.

Das obige ist der detaillierte Inhalt vonLogistische Regression, Klassifizierung: Überwachtes maschinelles Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!