Heim >Java >javaLernprogramm >Finden von Fibonacci-Zahlen mithilfe dynamischer Programmierung
Finden von Fibonacci-Zahlen mithilfe dynamischer Programmierung
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2024-07-17 00:12:31665Durchsuche
In diesem Abschnitt wird ein effizienter Algorithmus zum Ermitteln von Fibonacci-Zahlen mithilfe dynamischer Programmierung analysiert und entworfen. Abschnitt 18.3, Fallstudie: Berechnung von Fibonacci-Zahlen, gab eine rekursive Methode zum Ermitteln der Fibonacci-Zahl wie folgt an:
/**Die Methode zum Ermitteln der Fibonacci-Zahl*/
öffentliches statisches langes Fib (langer Index) {
if (index == 0) // Basisfall
return 0;
else if (index == 1) // Basisfall
return 1;
else // Reduktion und rekursive Aufrufe
return fib(index - 1) + fib(index - 2);
}
Wir können nun beweisen, dass die Komplexität dieses Algorithmus O(2^n) ist. Der Einfachheit halber sei der Index n. Lassen Sie T(n) die Komplexität für den Algorithmus bezeichnen, der fib(n) findet, und c die konstante Zeit für den Vergleich des Index mit 0 und 1 bezeichnen; das heißt, T(1) und T(0) sind c. Also

Ähnlich wie bei der Analyse des Tower-of-Hanoi-Problems können wir zeigen, dass T(n) O(2^n) ist.
Dieser Algorithmus ist jedoch nicht effizient. Gibt es einen effizienten Algorithmus zum Finden einer Fibonacci-Zahl? Das Problem mit der rekursiven fib-Methode besteht darin, dass die Methode redundant mit denselben Argumenten aufgerufen wird. Um beispielsweise fib(4) zu berechnen, werden fib(3) und fib(2) aufgerufen. Um fib(3) zu berechnen, werden fib(2) und fib(1) aufgerufen. Beachten Sie, dass fib(2) redundant aufgerufen wird. Wir können es verbessern, indem wir vermeiden, die Methode fib wiederholt mit demselben Argument aufzurufen. Beachten Sie, dass eine neue Fibonacci-Zahl durch Addition der beiden vorhergehenden Zahlen in der Folge erhalten wird. Wenn Sie die beiden Variablen f0 und f1 verwenden, um die beiden vorhergehenden Zahlen zu speichern, kann die neue Zahl f2 sofort durch Hinzufügen von f0 erhalten werden mit f1. Jetzt sollten Sie f0 und f1 aktualisieren, indem Sie f1 zu f0 und f2 zu f1 zuweisen , wie in der Abbildung unten gezeigt.

Die neue Methode ist im folgenden Code implementiert.
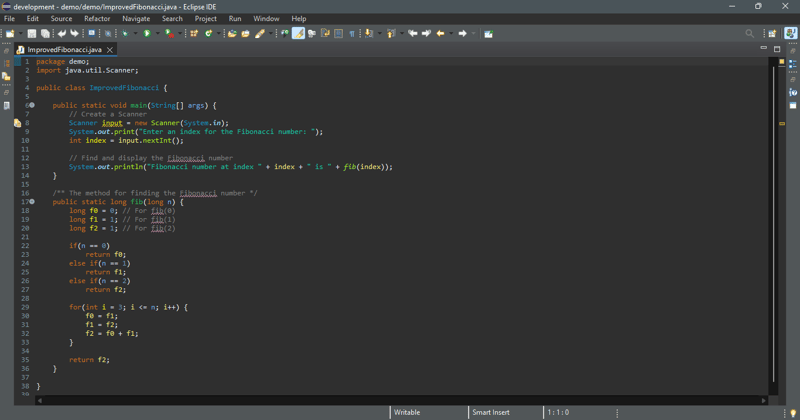
Geben Sie einen Index für die Fibonacci-Zahl ein: 6
Die Fibonacci-Zahl bei Index 6 ist 8
Geben Sie einen Index für die Fibonacci-Zahl ein: 7
Die Fibonacci-Zahl bei Index 7 ist 13
Offensichtlich beträgt die Komplexität dieses neuen Algorithmus O(n). Dies ist eine enorme Verbesserung gegenüber dem rekursiven O(2^n)-Algorithmus.
Der hier vorgestellte Algorithmus zur Berechnung von Fibonacci-Zahlen verwendet einen Ansatz, der als dynamische Programmierung bekannt ist. Bei der dynamischen Programmierung werden Teilprobleme gelöst und anschließend die Lösungen der Teilprobleme kombiniert, um eine Gesamtlösung zu erhalten. Dies führt natürlich zu einer rekursiven Lösung. Allerdings wäre die Verwendung der Rekursion ineffizient, da sich die Teilprobleme überschneiden. Die Grundidee der dynamischen Programmierung besteht darin, jedes Teilproblem nur einmal zu lösen und die Ergebnisse für die Teilprobleme zur späteren Verwendung zu speichern, um eine redundante Berechnung der Teilprobleme zu vermeiden.
Das obige ist der detaillierte Inhalt vonFinden von Fibonacci-Zahlen mithilfe dynamischer Programmierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

