Detaillierte Methode zum Finden der Wurzeln einer quadratischen Gleichung mit Geometry Sketchpad

Geometrie-Skizzenblock Finden Sie die Wurzeln quadratischer Gleichungen Das Lösen quadratischer Gleichungen ist ein häufiges Problem in der Mathematik. Geometry Sketchpad, eine geometrische Zeichensoftware, bietet eine effektive Möglichkeit, solche Gleichungen zu lösen. In diesem Artikel stellt der PHP-Editor Baicao den gesamten Prozess der Verwendung des geometrischen Skizzenblocks zum Finden der Wurzeln einer quadratischen Gleichung einer Variablen detailliert vor. In diesem Artikel wird Schritt für Schritt gezeigt, wie man den Graphen einer Gleichung erstellt, geometrische Eigenschaften nutzt und die genauen Werte der Wurzeln ableitet. Den Lesern wird empfohlen, die folgenden Details sorgfältig zu lesen, um die spezifischen Schritte und Techniken dieser Methode zu beherrschen.

Schritt 1: Öffnen Sie die Software und legen Sie drei Parameter fest. Klicken Sie im oberen Menü auf [Daten] und wählen Sie im Popup-Dropdown-Menü [Neuer Parameter] aus. Ändern Sie in dem kleinen Fenster, das sich öffnet, t1 in a, wählen Sie „Einheitslos“ aus, geben Sie den Standardwert ein und klicken Sie dann auf „OK“. Legen Sie auf die gleiche Weise die beiden anderen Parameter b und Parameter c fest. Lassen Sie ihre Werte zunächst 1 sein, und dann können Sie die Werte der Parameter nach Belieben ändern.

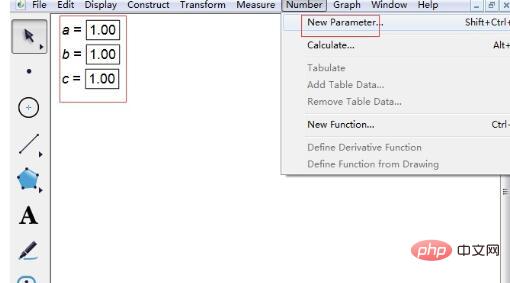
Schritt 2 Geben Sie den Funktionsausdruck der quadratischen Gleichung ein. Klicken Sie im oberen Menü auf [Zeichnen], wählen Sie die Option „Neue Funktion zeichnen“ und geben Sie den Ausdruck in das Popup-Dialogfeld ein. Bei der Eingabe von Ausdrücken sind einige Punkte zu beachten: 1. Klicken Sie bei der Eingabe von Parameter a mit der Maus auf das Multiplikationszeichen *, um x einzugeben.

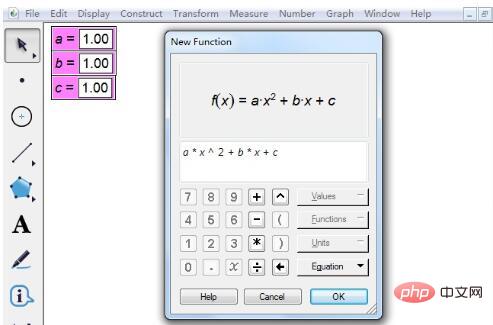
Schritt 3 Parameterwerte ändern. Klicken Sie nach der Eingabe des Ausdrucks auf [OK], um ein Diagramm wie unten gezeigt zu zeichnen. Offensichtlich hat es keinen Schnittpunkt mit der horizontalen Achse und die entsprechende quadratische Gleichung hat keine echten Wurzeln. Um den Wert des Parameters zu ändern, doppelklicken Sie auf Parameter a. Ein kleines Fenster wird angezeigt. Geben Sie einfach den spezifischen Wert ein.

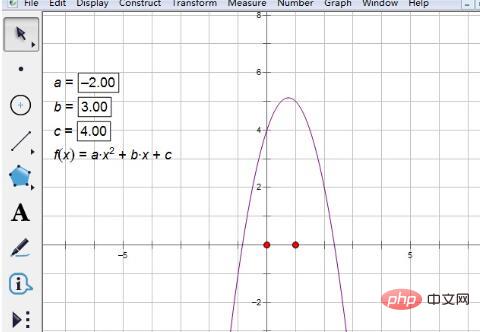
Schritt 4 Wählen Sie das Funktionswerkzeug aus. Klicken Sie in der linken Symbolleiste auf die Schaltfläche [Benutzerdefiniertes Tool] und wählen Sie aus der Popup-Verknüpfungsoption [Funktionstool] aus – die Wurzel von f(x)=0.

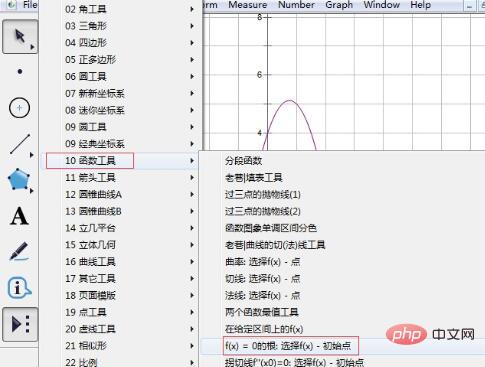
Schritt 5 Finden Sie die Wurzeln der Gleichung. Klicken Sie einmal auf den Funktionsanalyseausdruck, bewegen Sie den Cursor, und die Wurzelbeschriftung wird angezeigt, und eine Wurzel wird angezeigt. Klicken Sie erneut auf den Ausdruck, bewegen Sie den Cursor, eine weitere Wurzelbeschriftung wird angezeigt, und die zweite Wurzel wird angezeigt.

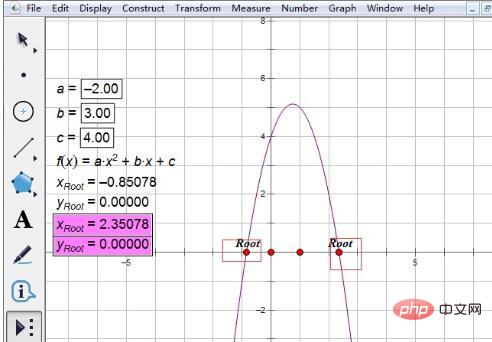
Tipps: Auf diese Weise wurden die beiden reellen Wurzeln der quadratischen Gleichung gefunden. Beachten Sie, dass die beiden x-Werte die Wurzeln sind und y die Ordinate ist. Wie findet man also die Wurzeln einer quadratischen Gleichung mit beliebigen Koeffizienten? Die Methode ist sehr einfach. Sie müssen lediglich auf die Parameter doppelklicken, die Werte von a, b und c ändern und die Wurzeln der neuen Gleichung werden sofort angezeigt.

Das obige ist der detaillierte Inhalt vonDetaillierte Methode zum Finden der Wurzeln einer quadratischen Gleichung mit Geometry Sketchpad. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!