Algorithmen und Beispiele zum Parsen von vier arithmetischen Ausdrücken in Javascript_Javascript-Kenntnissen

Beim Schreiben von Code stoßen wir manchmal auf Situationen, in denen wir selbst vier arithmetische Ausdrücke analysieren müssen. In diesem Artikel wird kurz die Verwendung von JavaScript zum Parsen einfacher vier arithmetischer Ausdrücke vorgestellt.

1. Bekannte Konzepte

Infix-Notation (oder Infix-Notation) ist eine allgemeine Methode zum Ausdrücken arithmetischer oder logischer Formeln. Der Operator steht in der Mitte der Operanden in Infix-Form (Beispiel: 3 4). Das heißt, unsere am häufigsten verwendeten arithmetischen Ausdrücke, Infix-Ausdrücke, sind für Menschen leichter zu verstehen, für Computer jedoch nicht einfach zu analysieren.

Umgekehrte polnische Notation (Umgekehrte polnische Notation, RPN oder umgekehrte polnische Notation) ist eine mathematische Ausdrucksmethode, die 1920 vom polnischen Mathematiker Jan Vukasiewicz eingeführt wurde. In der umgekehrten polnischen Notation werden alle Operatoren nach den Operanden platziert , daher wird es auch Suffix-Notation genannt. Bei der umgekehrten polnischen Notation sind keine Klammern erforderlich, um den Vorrang des Operators anzuzeigen. Die umgekehrte polnische Notation erleichtert die Verwendung einer Stapelstruktur zum Parsen und Berechnen von Ausdrücken. Daher analysieren wir hier vier Elementausdrücke, indem wir zunächst den Infix-Ausdruck in einen umgekehrten polnischen Ausdruck konvertieren. Berechnen Sie dann den Wert.

2. Konvertierungsprozess

Infix-Ausdruck in Postfix-Ausdruck konvertieren (Planungsfeldalgorithmus)

1. In der Eingabewarteschlange erscheint eine Markierung
2. Wenn es sich bei dem Token um eine Zahl handelt, fügen Sie sie der Ausgabewarteschlange hinzu
3. Wenn es sich um einen Operator (-*/) handelt, vergleichen Sie ihn mit dem Operator oben auf dem Ausgabestapel. Wenn die Priorität kleiner oder gleich der des Operators oben auf dem Stapel ist, platzieren Sie den Operator oben des Stapels und fügen Sie ihn der Ausgabewarteschlange hinzu (Schleife, bis die oben genannten Bedingungen nicht mehr erfüllt sind) und schieben Sie diesen Operator schließlich auf den Stapel.
4. Wenn es sich um eine linke Klammer handelt, schieben Sie sie auf den Stapel
5. Wenn es sich um eine rechte Klammer handelt, entfernen Sie fortlaufend Operatoren aus dem Stapel und fügen Sie sie der Ausgabewarteschlange hinzu, bis das Element oben im Stapel die linke Klammer ist. Öffnen Sie die linke Klammer und fügen Sie sie nicht zur Ausgabewarteschlange hinzu. Wenn die linke Klammer nicht gefunden wird, bedeutet dies, dass die Klammern im ursprünglichen Ausdruck nicht symmetrisch sind und ein Fehler vorliegt.
6. Wenn die Eingabewarteschlange leer ist und sich noch Operatoren auf dem Stapel befinden und der Operator oben auf dem Stapel eine linke Klammer ist, bedeutet dies, dass der ursprüngliche Ausdruck nicht übereinstimmende Klammern enthält. Entfernen Sie die Operatoren nacheinander vom Stapel und fügen Sie sie der Ausgabewarteschlange hinzu.
7. Füllen Sie
aus

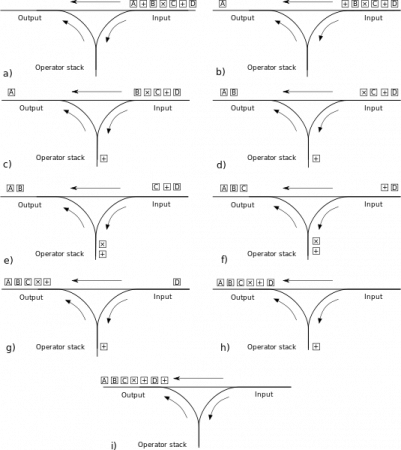
3. Implementierung der Codekonvertierung

function isOperator(value){
	var operatorString = "+-*/()";
	return operatorString.indexOf(value) > -1
}

function getPrioraty(value){
	switch(value){
		case '+':
		case '-':
			return 1;
		case '*':
		case '/':
			return 2;
		default:
			return 0;
	}
}

function prioraty(o1, o2){
	return getPrioraty(o1) <= getPrioraty(o2);
}

function dal2Rpn(exp){
	var inputStack = [];
	var outputStack = [];
	var outputQueue = [];

	for(var i = 0, len = exp.length; i < len; i++){
		var cur = exp[i];
		if(cur != ' ' ){
			inputStack.push(cur);
		}
	}
	console.log('step one');
	while(inputStack.length > 0){
		var cur = inputStack.shift();
		if(isOperator(cur)){
			if(cur == '('){
				outputStack.push(cur);
			}else if(cur == ')'){
				var po = outputStack.pop();
				while(po != '(' && outputStack.length > 0){
					outputQueue.push(po);
					po = outputStack.pop();
				}
				if(po != '('){
					throw "error: unmatched ()";
				}
			}else{
				while(prioraty(cur, outputStack[outputStack.length - 1]) && outputStack.length > 0){
					outputQueue.push(outputStack.pop());
				}
				outputStack.push(cur);
			}
		}else{
			outputQueue.push(new Number(cur));
		}
	}
	console.log('step two');
	if(outputStack.length > 0){
		if(outputStack[outputStack.length - 1] == ')' || outputStack[outputStack.length - 1] == '('){
			throw "error: unmatched ()";
		}
		while(outputStack.length > 0){
			outputQueue.push(outputStack.pop());
		}
	}
	console.log('step three');
	return outputQueue;

}

console.log(dal2Rpn('1 + 2'));
console.log(dal2Rpn('1 + 2 + 3'));
console.log(dal2Rpn('1 + 2 * 3'));
console.log(dal2Rpn('1 + 2 * 3 - 4 / 5'));
console.log(dal2Rpn('( 1 + 2 )'));

console.log(dal2Rpn('( 1 + 2 ) * ( 3 - 4 ) / 5'));
console.log(dal2Rpn('( 1 + 2 ) * (( 3 - 4 ) / 5)'));

4. Bewertung des umgekehrten polnischen Ausdrucks

1. Nehmen Sie einen Token aus der Eingabewarteschlange
2. Wenn es sich um einen Operanden handelt, fügen Sie ihn dem Ausgabestapel
hinzu 3. Wenn es sich um einen Operator handelt, entfernen Sie die beiden Operanden vom Ausgabestapel, führen Sie Berechnungen durch und verschieben Sie den berechneten Wert auf den Ausgabestapel.
4. Schleifenbetrieb: Wenn die Eingabewarteschlange leer ist und der Ausgabestapel nur eine Nummer hat, ist diese Nummer das Ergebnis, andernfalls gibt es redundante Operanden.

5. Berechnungscode

function evalRpn(rpnQueue){
	var outputStack = [];
	while(rpnQueue.length > 0){
		var cur = rpnQueue.shift();

		if(!isOperator(cur)){
			outputStack.push(cur);
		}else{
			if(outputStack.length < 2){
				throw "unvalid stack length";
			}
			var sec = outputStack.pop();
			var fir = outputStack.pop();

			outputStack.push(getResult(fir, sec, cur));
		}
	}

	if(outputStack.length != 1){
		throw "unvalid expression";
	}else{
		return outputStack[0];
	}
}

6. Fazit

Die umgekehrte polnische Notation ist nichts, woran Sie gewöhnt sind, wenn Sie zum ersten Mal damit in Kontakt kommen, aber nachdem Sie sich damit vertraut gemacht haben, werden Sie feststellen, dass die Idee eigentlich sehr einfach ist, im Gegensatz zur Infix-Notation, die verschiedene Prioritäten hat und Klasse, die Logik ist besonders problematisch, aber die umgekehrte polnische Notation ist prägnanter, es besteht überhaupt keine Notwendigkeit, die Priorität zu berücksichtigen, und es besteht keine Notwendigkeit, die Situation durch Klammern, eckige Klammern und geschweifte Klammern zu stören.