16开始接触前端,一直对一个问题特别感兴趣,那就是js动画,也就是从那时起开始探究动画的各种表现形式,也是那个时候开始意识到编程这块东西最终考验的就是抽象和逻辑,而这一切完全是数学里边的东西。
最早接触tweenJS是去年还是前年来着有点忘了,不过当时有点不大看得懂,勉勉强强算是过了一遍,不过有了这个体验之后,我自己做了一套项目,里边有个返回顶部按钮,当鼠标按下时,我使用了sin函数控制阴影的大小,具体效果表现还着实惊艳了自己一番,就像呼吸灯那样,于是在那以后的各种面试会上,我都乐此不彼的给面试官展示我的项目。现在想想觉得还是有趣极了。
有点扯远了,现在来说说tweenJS,因为我很懒所以下面会使用TT代表tweenJS。TT其实是一个非常小巧的动画库--体积小代码又精炼,然而他所能实现的各种效果确实很多。那最简单的线性运动来说,代码如下
/*
* @param { number } t (当前次数)
* @param { number } b beginning value(初始值)
* @param { number } c change in value(变化量)
* @param { number } d (动画次数)
*/
function(t, b, c, d) {
return c * t / d + b;
}先不说上面的代码,我这里想讨论一下动画,其实一个动画就是起点到终点某个元素的某个属性随着时间逐渐改变的过程,无论这个属性是距离,颜色,大小,everything,只要能随时间改变,我们就可以称之为动画。现在再看上边的代码,为了便于讨论方便b也就是动画的起点我们可以设置为0,所以现在我们以距离为例讨论一下这个函数。b为0,那么决定最终位置的就是c,d(是持续时间),t。大家可以想想初中我们学到的公式:路程 / 时间 = 速度,所以在上边的公式里,c/d 是一个常量,而唯一变化的时间t,配合速度相乘,就是确定在某一个时间点上该物体应该所在的位置,而随着时间逐渐改变t之后,就会产生一个动画,举例如下:
实例
<style>
.example{
width:120px;
height:20px;
background:#000;
}
</style>
<div id="test" class="example"></div>
<script>
function linear(t, b, c, d) {
return c * t / d + b;
}
//我们在这里要让div#test向下移动一100px,持续时间是2s,这里注意一下间隔的
//算法,总共需要运行10次才能到达100px 的位置,所以间隔的算法为 2000 / 10 = 200ms/次,
// 块级作用域里,t从 0 - 10 ,每一次for循环启动一个定时器,分别从0,200,400,600,2000后设置marginTop的值
for( let t = 0;t <=10;t++ )
setTimeout(
function(){
test.style.marginTop = linear( t,0,100,10 ) + 'px'
},
200*t
)
</script>在制作web动画时,有一个要求是,60fps准则,那么我们每次时间间隔因为 1000/ 60 ,这样的话t 每次的变化量就可以写成 t += 1000/60 ,其他条件不变,因此总共持续的次数就是 2000 / (1000/60),代码可以写成这样:
function linear(t, b, c, d) {
return c * t / d + b;
}
for( let t = 0;t <=2000;t += (1000/60) )
setTimeout(
function(){
let curT = Math.floor(t/(1000/60));
test.style.marginTop = linear( curT,0,100,2000/(1000/60) ) + 'px'
},
t
)当然啦,现在推荐requestAnimationFrame这个window的api,所以尽量用这个,当然基本算法还是差不多的。
再来看一个Sine.easeIn:
/*
* @param { number } t (当前次数)
* @param { number } b beginning value(初始值)
* @param { number } c change in value(变化量)
* @param { number } d (动画次数)
*/
function SinEaseIn(t, b, c, d) {
return -c * Math.cos(t/d * (Math.PI/2)) + c + b;
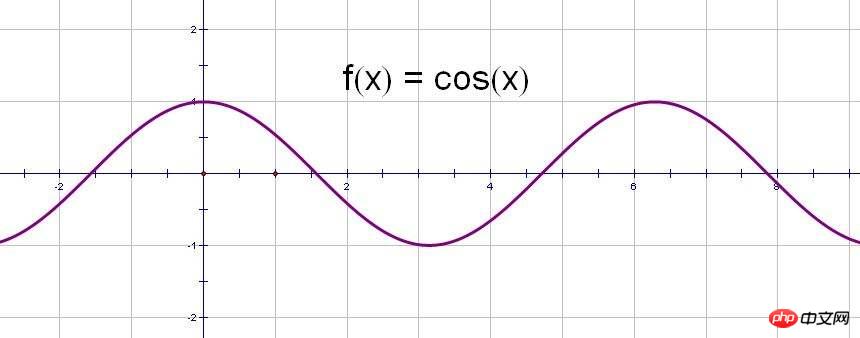
}仍以距离为例,b我们也设置为0,更方便弄懂,cos函数在 0 -- (t/d)*0.5π上的变化范围为 1 -- cos((t/d)*0.5π),t/d <=1,
即 为 1 -- cos(0.5π) => 1 -- 0 所以,正好是cos函数的四分之一个周期,我下面找个图,看着更清晰:
![]()
所以SinEaseIn 函数的返回值会从 0 - c变化 ,最后到达最终位置。

