详解K路归并排序(实战)
- 藏色散人 转载
- 2021-07-14 14:10:08 3648浏览
引入:
其实K路归并排序的用处还是很广的,最简单的,假设你要排序海量的数据,比如TB级别的数据(我们姑且说是TB级别的搜索关键字),但是我们的内存只有GB级别,我们没办法一次把所有的数据全部载入然后排序,但是我们的确最终要结果,那么怎么办呢?K路归并排序闪亮登场 ,其实这就是一个“分而治之”的思想,既然我们要排Q个数,但是我们不能一次头全部排序完毕,这时候,我们把Q分为k组,每组n 个数,(k 分析: (1)如何合并k个已经排序了的数组呢? 因为我们以前讨论过堆,显然堆的排序效率是非常高的,所以我们自然也考虑到用堆来实现,因为要升序排列,所以我们创建一个最小堆。因为最终排序结果的数总是小的在前面大的在后面,所以我们考虑先把所有的n个数组的第一个元素(最小数)都放入最小堆中,所以最小堆的大小为k。这样我们调整堆结构,那么它的第一个元素就是min( min(array1),min(array2)....min(arrayn))显然就是所有数中的最小元素。 (2)因为在任意数组中都是按照升序排列的,所以我们一旦从堆中删除了一个最小元素,就必须找一个元素来填这个坑。为此,我们需要找到删除元素所在的数组中的下一个元素然后将其填入堆。(这个有点像是吧全国的最精英的士兵都拉去精英团打仗,那么就是每个团的最强的都拉来,如果这个人不幸战死,那么从同团中找出仅次于它的继续顶这个精英团,这样永远保持精英团的战斗力最高) 所以,如何去根据被删除的堆元素找这个被删除的堆元素所在的数组呢?这就需要在我们新建一个复合类型,它既包括当前的值,也包含这个当前值所在的数组的id, (3)因为每个排序了的数组,随着最小的元素的不断流失,它还没有参与排序的值是渐渐变少的,所以我们必须维护一个长度为k的数组,这个数组保留了每个数组中还没参与排序的当前位置。并且一旦这个数组中剩余的最小元素被添加到了堆,那么这个当前位置必须后移。 (4)随着每个数组的当前位置后移,总归最后会达到这个数组的末端,这时候,这个数组就不能再提供任何数了,(这个很正常,比如部队中有一个尖刀连,它包含了最杰出的人,那么最后选到精英团时,总从这个连队选,然后这个连队一定最后没人了) ,所以我们就无法从当前删除的数所在数组中找到下一个值了,这时候我们就必须选择下一个有值的数组id,并且挑选出其最小值,方法是arrayIdForDeletedData = (arrayIdForDeletedData + 1) % k 。 (5)最后总有所有的数组位置都到了末端,也就是所有数组都不能提供未参与排序的值,所以这时候我们就要判断当前的堆是否为空,如果不为空,那么他们就包含了n*k中的最大的几个数了,我们依次deleteMin()来吧最大的几个数按照最小顺序输出。如果当前的堆已经为空,那么直接跳出循环。 所以最终时间复杂仅为 O(n*logk) 代码: 想清楚了上述几个关键技术细节,这里代码就很好写了。 首先,我们定义一个值对象,它封装了某个整数以及这个整数来自于哪个数组. 然后我们定义一个最小堆,它是解决问题的关键,需要注意的是,它包含的元素应该是上述的值对象,当入堆,调整堆,基于的计算都是值对象的data字段。 最后,我们来实现K路合并器,还是挺好实现的,不过涉及到一些下标运算必须特别小心。因为我们要通用,所以k和n都是传进来的,实际上,我们如果事先规划好k和n之后,完全不用在内部维护这些数,因为只要吧他们存入最小堆就行了。 实验: 最后我们来演示下,假设我们有32个数,我们分为4路合并,每路8个数,并且这8个数是已经排序的。 然后我们用K路合并算法来对所有的32个数进行排序: 最后运行结果为: 显然结果是正确的,而且我们的方法是支持重复的值的。package com.charles.algo.kwaymerge;
/**
*
* 这个对象表明是一个可以跟踪来自于哪个数组的数据对象
* @author charles.wang
*
*/
public class TrackableData {
//data表明具体的值
private int data;
//comeFromArray表明这个值来自于哪一个数组
private int comeFromArray;
public TrackableData(int data,int comeFromArray){
this.data = data;
this.comeFromArray=comeFromArray;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public int getComeFromArray() {
return comeFromArray;
}
public void setComeFromArray(int comeFromArray) {
this.comeFromArray = comeFromArray;
}
}package com.charles.algo.kwaymerge;
/**
* @author charles.wang
*
*/
public class MinHeap {
// 最小堆的存储是一个数组,并且为了计算,我们第一个位置不放内容
private TrackableData[] data;
// 堆的大小
private int heapSize;
// 当前元素的数量
private int currentSize;
public MinHeap(int maxSize) {
heapSize = maxSize;
// 创建一个比最大容纳数量多1的数组的作用是启用掉数组的头元素,为了方便运算,因为从1开始的运算更加好算
data = new TrackableData[heapSize + 1];
currentSize = 0;
}
/**
* 返回当前的堆是否为空
* @return
*/
public boolean isEmpty(){
if(currentSize==0)
return true;
return false;
}
/**
* 这里考察堆的插入,因为最小堆内部结构中数组前面元素总是按照最小堆已经构建好的,所以我们总从尾部插入 解决方法是: Step
* 1:先把当前的元素插入到数组的尾部 Step 2:递归的比较当前元素和父亲节点元素, Step
* 3:如果当前的元素小于父亲节点的元素,那么就把当前的元素上移,直到移不动为止
*
* @param value
* @return
*/
public MinHeap insert(TrackableData value) {
// 首先判断堆是否满了,如果满了就无法插入
if (currentSize == heapSize)
return this;
// 如果堆还没有满,那么说明堆中还有位置可以插入,我们先找到最后一个可以插入的位置
// currentPos表示当前要插入的位置的数组下标
int currentPos = currentSize + 1;
// 先插入到当前的位置,因为是从1开始的,所以数组下标运算也要+1
data[currentPos] = value;
// 然后比较当前元素和他的父亲元素
// 当前元素是data[currentPos] ,父亲元素是 data[(currentPos/2],一直遍历到根
TrackableData temp;
// 如果currentPos为1,表明是插入的堆中第一个元素,则不用比较
// 否则, 如果插了不止一个元素,则用插入位置的元素和其父元素比较
while (currentPos > 1) {
// 如果当前元素小于父亲元素,那么交换他们位置
if (data[currentPos].getData() < data[currentPos / 2].getData()) {
temp = data[currentPos / 2];
data[currentPos / 2] = data[currentPos];
data[currentPos] = temp;
// 更新当前位置
currentPos = currentPos / 2;
}
// 否则, 在假定已有的堆是最小堆的情况下,说明现在插入的位置是正确的,不用变换
else {
break;
}
}
// 插入完毕之后,吧当前的堆中元素的个数加1
currentSize++;
return this;
}
/**
* 这里考察堆的删除 因为是最小堆,所以肯定删除最小值就是删除堆的根元素,此外,还必须要调整剩余的堆使其仍然保持一个最小堆
* 因为有删除最小元素之后最小元素位置就有了个空位,所以解决方法是: Step 1:吧堆中最后一个元素复制给这个空位 Step
* 2:依次比较这个最后元素值,当前位置的左右子元素的值,从而下调到一个合适的位置 Step 3:从堆数组中移除最后那个元素
*/
public TrackableData deleteMin() {
// 如果最小堆已经为空,那么无法删除最小元素
if (currentSize == 0)
return null;
// 否则堆不为空,那么最小元素总是堆中的第一个元素
TrackableData minValue = data[1];
// 既然删除了最小元素,那么堆中currentSize的尺寸就要-1,为此,我们必须为数组中最后一个元素找到合适的新位置
// 堆中最后一个元素
TrackableData lastValue = data[currentSize];
// 先将堆中最后一个元素移动到最小堆的堆首
data[1] = lastValue;
// 把堆内部存储数组的最后一个元素清0
data[currentSize] = null;
// 并且当前的堆的尺寸要-1
currentSize--;
// 现在开始调整堆结构使其仍然为一个最小堆
int currentPos = 1; // 当前位置设置为根,从根开始比较左右
int leftPos = currentPos * 2;
TrackableData leftValue;
TrackableData rightValue;
TrackableData temp;
// 如果左位置和当前堆的总容量相同,说明只有2个元素了,一个是根元素,一个是根的左元素
if (leftPos == currentSize) {
// 这时候如果根左元素data[2]比根元素data[1]小,那么就交换二者位置
if (data[2].getData() < data[1].getData()) {
temp = data[2];
data[2] = data[1];
data[1] = temp;
}
}
else {
// 保持循环的条件是该节点的左位置小于当前堆中元素个数,那么该节点必定还有右子元素并且位置是左子元素位置+1
while (leftPos < currentSize) {
// 获取当前位置的左子节点的值
leftValue = data[leftPos];
// 获取当期那位置的右子节点的值
rightValue = data[leftPos + 1];
// 如果当前值既小于左子节点又小于右子节点,那么则说明当前值位置是正确的
if (data[currentPos].getData() < leftValue.getData()
&& data[currentPos].getData() < rightValue.getData()) {
break;
}
// 否则,比较左子节点和右子节点
// 如果左子节点小于右子节点(当然了,同时小于当前节点),那么左子节点和当前节点互换位置
else if (leftValue.getData() < rightValue.getData()) {
temp = data[currentPos];
data[currentPos] = leftValue;
data[leftPos] = temp;
// 同时更新当前位置是左子节点的位置,并且新的左子节点的位置为左子节点的左子节点
currentPos = leftPos;
leftPos = currentPos * 2;
}
// 如果右子节点小于左子节点(当然了,同时小于当前节点),那么右边子节点和当前节点互换位置
else {
temp = data[currentPos];
data[currentPos] = rightValue;
data[leftPos + 1] = temp;
// 同时更新当前位置是右子节点的位置,并且新的左子节点的位置为右子节点的左子节点
currentPos = leftPos + 1;
leftPos = currentPos * 2;
}
}
}
return minValue;
}
}package com.charles.algo.kwaymerge;
import java.util.ArrayList;
import java.util.List;
/**
*
* 这个类用于演示K路合并
*
* @author charles.wang
*
*/
public class KWayMerger {
private KWayMerger() {
}
/**
* k路合并,这里的指导思想如下:
*
* (1)首先构造一个最小堆,其中堆中的元素初始值为每个数组中的最小元素
* (2)每次从最小堆中打印并且删除最小元素,然后把这个最小元素所在的数组中的下一个元素插入到最小堆中 (3)每次(2)结束后调整堆来维持这个最小堆
*/
public static void mergeKWay(int k, int n, List<int[]> arrays) {
// 这里存储了所有每个数组的当前的下标,在没有开始插入之前,每个数组的当前下标都设为0
int[] indexInArrays = new int[k];
for (int i = 0; i < k; i++) {
indexInArrays[i] = 0;
}
// 首先构造一个最小堆,其大小为k
MinHeap minHeap = new MinHeap(k);
// 第一步,依次吧每个数组中的第一个元素都插入到最小堆
// 然后把所有数组的下标都指向1
for (int i = 0; i < k; i++) {
// 这里每个都构造TrackableData对象:
// 其中:arrays.get(i)[0]表示它值为第i个数组的下标为0的元素(也就是第i个数组的第一个元素)
// i表示这个对象来自于第i个数组
minHeap.insert(new TrackableData(arrays.get(i)[0], i));
indexInArrays[i] = 1;
}
// 第二步,对最小堆进行反复的插入删除动作
TrackableData currentDeletedData;
TrackableData currentInsertedData;
int arrayIdForDeletedData;
int nextValueIndexInArray;
// 循环的条件是k个数组中至少有一个还有值没有被插入到minHeap中
while (true) {
// 这个变量维护了有多少个数组当前下标已经越界,也就是数组所有元素已经被完全处理过
int noOfArraysThatCompletelyHandled = 0;
// 就是去查询维护所有数组当前下标的数组,如果都越界了,那么就说明都比较过了
for (int i = 0; i < k; i++) {
if (indexInArrays[i] == n)
noOfArraysThatCompletelyHandled++;
}
// 如果所有的数组中的所有的值都比较过了,那么查看堆中内容是否为空。
if (noOfArraysThatCompletelyHandled == k) {
while (!minHeap.isEmpty()) {
currentDeletedData = minHeap.deleteMin();
// 打印出当前的数
System.out.print(currentDeletedData.getData() + " ");
}
break;
}
currentDeletedData = minHeap.deleteMin();
// 打印出当前的数
System.out.print(currentDeletedData.getData() + " ");
// 获取当前的被删的数来自于第几个数组
arrayIdForDeletedData = currentDeletedData.getComeFromArray();
// 获取那个数组的当前下标
nextValueIndexInArray = indexInArrays[arrayIdForDeletedData];
// 如果当前下标没有越界,说明当前数组中还有元素,则找到该数组中的下个元素
if (nextValueIndexInArray < n) {
// 构造新的TrackableData,并且插入到最小堆
currentInsertedData = new TrackableData(
arrays.get(arrayIdForDeletedData)[nextValueIndexInArray],
arrayIdForDeletedData);
minHeap.insert(currentInsertedData);
// 同时更新维护数组当前下标的数组,让对应数组的当前下标+1
indexInArrays[arrayIdForDeletedData]++;
}
// 如果当前下标已经越界,说明这个数组已经没有任何元素了,则找下一个有值的数组的最小元素
else {
while (true) {
arrayIdForDeletedData = (arrayIdForDeletedData + 1) % k;
// 获取那个数组的当前下标
nextValueIndexInArray = indexInArrays[arrayIdForDeletedData];
if (nextValueIndexInArray == n)
continue;
else {
// 构造新的TrackableData,并且插入到最小堆
currentInsertedData = new TrackableData(
arrays.get(arrayIdForDeletedData)[nextValueIndexInArray],
arrayIdForDeletedData);
minHeap.insert(currentInsertedData);
// 同时更新维护数组当前下标的数组,让对应数组的当前下标+1
indexInArrays[arrayIdForDeletedData]++;
break;
}
}
}
}
}
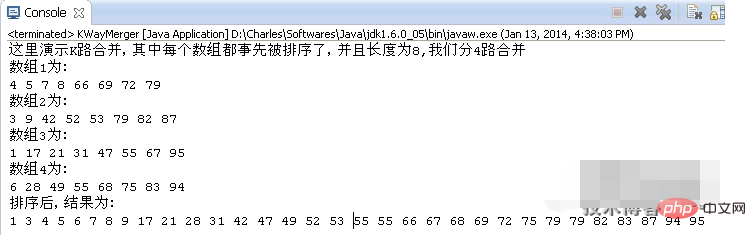
}public static void main(String[] args) {
// 我们来演示K路合并,假设我们有4组已经排序了的数组,每组有8个数,则n=8,k=4
int[] array1 = { 4, 5, 7, 8, 66, 69, 72, 79 };
int[] array2 = { 3, 9, 42, 52, 53, 79, 82, 87 };
int[] array3 = { 1, 17, 21, 31, 47, 55, 67, 95 };
int[] array4 = { 6, 28, 49, 55, 68, 75, 83, 94 };
System.out.println("这里演示K路合并,其中每个数组都事先被排序了,并且长度为8,我们分4路合并");
System.out.println("数组1为:");
for(int i=0;i<array1.length;i++)
System.out.print(array1[i]+" ");
System.out.println();
System.out.println("数组2为:");
for(int i=0;i<array2.length;i++)
System.out.print(array2[i]+" ");
System.out.println();
System.out.println("数组3为:");
for(int i=0;i<array3.length;i++)
System.out.print(array3[i]+" ");
System.out.println();
System.out.println("数组4为:");
for(int i=0;i<array4.length;i++)
System.out.print(array4[i]+" ");
System.out.println();
List<int[]> arrayLists = new ArrayList<int[]>(4);
arrayLists.add(0, array1);
arrayLists.add(1, array2);
arrayLists.add(2, array3);
arrayLists.add(3, array4);
KWayMerger kWayMerger = new KWayMerger(4, 8, arrayLists);
System.out.println("排序后,结果为:");
kWayMerger.mergeKWay();
System.out.println();
}